New concept of assessment of system solid / liquid / vapor at wetting (EN) / Новая концепция оценки системы твердое тело / жидкость / пар при смачивании (RU)
В. К. Верхоломов
Аннотация
Показано, что по основным физическим характеристикам систему твердое тело / жидкость / пар нельзя рассматривать как термодинамическую. Она является разновидностью механической системы.
// Наука и мир. 2017, № 10, V. 1, с. 11-15.
Введение
Как известно [1, 3, 7 и др.], смачивание жидкой фазой твердой поверхности определяется физико-химическими процессами на границах раздела фаз, участвующих в смачивании.
Важной характеристикой в теории смачивания является величина равновесного краевого угла смачивания. Накопленные к настоящему времени многочисленные экспериментальные данные по краевым углам смачивания входят в противоречие с некоторыми положениями теории смачивания. Из анализа последних следует наличие двух подходов для оценки системы твердое тело / жидкость / пар и, соответственно, для определения краевого угла смачивания θ0: механический и термодинамический. Как уже указывалось в работе [2], родоначальником механического подхода (механической модели) был Т. Юнг, родоначальником термодинамического – У. Гиббс.
В соответствии с современной теорией смачивания одновременно сосуществуют и считаются правильными оба подхода: и механический, и термодинамический. Тем не менее, термодинамический подход считается определяющим, основным. На его основе было получено уравнение равновесного краевого угла – уравнение Юнга. Ниже будет показано, что имеющиеся эксперименты дают серьезные основания усомниться в правильности уравнения Юнга.
В соответствии с новой предлагаемой концепцией такое положение, когда признаются правильными оба подхода, считается неприемлемым, ибо оба подхода являются взаимоисключающими друг друга. Ведь это является аксиомой: если рассматриваемая система твердое тело / жидкость / пар является термодинамической, то нельзя применять законы и положения механики, а если механической – законы термодинамики. Одно из двух: или рассматриваемая система – термодинамическая, или она – разновидность механической системы. Целями настоящей работы была попытка еще раз проанализировать оба подхода и на основании такого анализа сделать окончательный выбор.
Сегодняшнее положение таково, что во всей литературе исследуемая система рассматривается как термодинамическая. Поэтому наш анализ начнем с рассмотрения системы твердое тело / жидкость / пар в качестве термодинамической системы. Но вначале рассмотрим уравнение Юнга и его корреляцию с имеющимися экспериментами.
1. Экспериментальная оценка корреляции величин краевого угла и поверхностной энергии твердого тела
Как известно, для изолированной термодинамической системы выполняется одно из основных положений термодинамики: в состоянии равновесия системы ее потенциальная энергия минимальна. На основании такого термодинамического подхода было получено уравнение равновесного краевого угла – уравнение Юнга
Cosθ0=(σSV - σSL)/ σLV, (1)
где σSV, σSL – величины поверхностных энергий на границах твердое тело / пар и твердое тело / жидкость соответственно; σLV – величина поверхностной энергии на границе жидкость / пар (энергия поверхностного натяжения).
Значительным достижением последнего времени в теории поверхностных явлений, связанных с процессами смачивания, явилась разработка молекулярной теории смачивания Джирифалко – Гуда – Фоукса [9, 10]. В рамках этой теории удельная свободная поверхностная энергия на границе раздела фаз представляет сумму дисперсионной и полярной составляющих. Дисперсионная составляющая соответствует дисперсионным межмолекулярным силам взаимодействия. Полярная составляющая соответствует остальным межмолекулярным силам взаимодействия (ориентационные, индукционные взаимодействия, водородные связи и др.). Так, например, для поверхностной энергии на границе твердое тело/пар
σSV = σSVd + σSVp, (2)
где σSVd, σSVp – дисперсионная и полярная составляющие поверхностной энергии на границе твердое тело / пар соответственно.
В работе [10] получена зависимость величины поверхностной энергии на границе твердое тело / жидкость σSL от составляющих (дисперсионной и полярной) поверхностных энергий твердого тела и жидкости. Поэтому, в соответствии с уравнением (1), краевой угол смачивания должен быть функцией поверхностных энергий на границах твердое тело / пар и жидкость / пар, т.е. θ0(Cosθ0)= f(σSV, σLV). Если капли одной и той же жидкости (например, воды) нанести на различные твердые низкоэнергетические поверхности, то краевой угол должен зависеть только от поверхностной энергии на границе твердое тело/пар, т.е. θ0 = f(σSV). Для подтверждения наличия такой зависимости обратимся к экспериментальным данным.
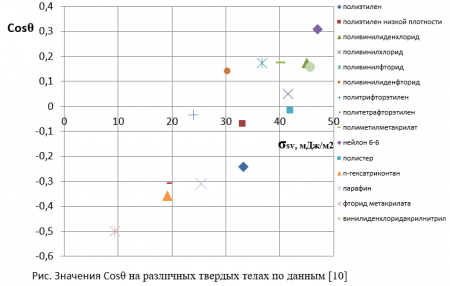
На рис. приведены значения Cosθ0 (в области относительно высоких значений θ0>600), полученные на основании экспериментальных данных работы [10] при смачивании водой полимеров с различными величинами σSV. Можно отметить, что здесь представлена лишь небольшая часть имеющихся в литературе экспериментальных данных. Как следует из рис., экспериментальные точки легли с большим разбросом: погрешность разброса доходит до 50 %. Это делает практически невозможным получить с приемлемой погрешностью однозначную зависимость между величинами Cosθ0 и σSV.
Таким образом, имеющиеся в литературе экспериментальные данные не подтверждают однозначную зависимость между величинами Cosθ0 и σSV.
Об этом же свидетельствуют результаты расчетных исследований. В работе [11] показано, что в случае смачивания одной и той же жидкостью (σLV = Const) определённое значение равновесного краевого угла получается на бесконечно большом количестве твердых поверхностей, различающихся значениями σSV.
Из всего этого следует, что классическое уравнение Юнга, полученное на основании термодинамического подхода, не работает. Поэтому уравнение краевого угла смачивания требует серьезного пересмотра. И такой пересмотр был сделан в работе [12]. В результате было получено новое уравнение (уравнение Юнга-Верхоломова) равновесного краевого угла смачивания.
Далее остановимся на главном вопросе, можно ли считать систему твердое тело / жидкость / пар термодинамической системой.
2. Система твердое тело / жидкость / пар, как термодинамическая система
Рассмотрим систему твердое тело / жидкость / пар в качестве термодинамической системы. И если удастся доказать, что рассматриваемая система является термодинамической, то второй подход (механический) отпадает автоматически. И наоборот: если не удастся это доказать, то систему следует признать механической.
Прежде всего, целесообразно напомнить [4], что под термодинамической системой понимается материальная система, каждое взаимодействие которой с окружающей средой состоит из теплопередачи или связано с совершением работы системой или над системой. В общем случае термодинамическая система может быть многофазной. Именно к таким системам относится исследуемая трехфазная система твердое тело / жидкость / пар. Термодинамический процесс, т.е. переход системы из одного состояния в другое, подчиняется двум закономерностям: во-первых, закону сохранения энергии и, во-вторых, уравнению состояния F(P,V,T). При этом любой термодинамический процесс можно описать линией на графике в термодинамических координатах в соответствии с уравнением состояния.
В общем случае уравнение закона сохранения энергии (первое начало термодинамики) для бесконечно малого термодинамического процесса имеет вид [4]:
dE = dQ – d A +∑ µi dni, (3)
где E – внутренняя энергия системы; Q – тепло, подведенное к системе из окружающей среды; A – механическая работа, отведенная от системы в окружающую среду; µi – химический потенциал iго компонента системы; ni – количество молей iго компонента системы.
Здесь необходимо сделать следующее пояснение. Термодинамическая система имеет границы (в частном случае это может быть некоторая контрольная поверхность, включающая все взаимодействующие тела системы), которые отделяют ее от окружающей, внешней среды и через которые происходит взаимодействие между системой и окружающей средой. Каждую многофазную систему можно представить, как совокупность соответствующих двухфазных систем [6]. Рассматриваемая трехфазная система твердое тело / жидкость / пар состоит из трех подсистем, каждая из которых является двухфазной: твердое тело/пар, твердое тело/жидкость и жидкость/пар. Внутренняя энергия исследуемой системы представляет сумму энергий двухфазных систем:
E = ESV + ESL + ELV, (4)
где ESV – внутренняя энергия двухфазной системы твердое тело/пар; ESL, ELV – внутренние энергии двухфазных систем твердое тело / жидкость и жидкость / пар соответственно.
Внутренняя энергия каждой двухфазной системы состоит из энергий объемов отдельных фаз и энергии на поверхностях раздела фаз.
Итак, мы рассматриваем процесс растекания капли жидкости по поверхности твердого тела, как термодинамический процесс. Примем следующие допущения: рассматриваемая система является изолированной; процесс растекания капли жидкости является физическим (нет химических реакций, процессов растворения и др.) и изотермическим (T= Const); жидкость однокомпонентная и несжимаемая (V= Const); состав системы в процессе растекания капли жидкости не меняется ni= Const.
Поскольку процесс растекания капли жидкости по поверхности твердого тела является изолированным, подвод тепла из окружающей среды отсутствует (dQ =0) и механическая работа в окружающую среду не отводится (и не подводится) (dA=0). Так как состав системы не меняется, то dni=0. В итоге из уравнения (3) следует, что в процессе растекания капли жидкости изменения внутренней энергии системы не происходит: dE=0, т.е.
E = Const. (5)
Таким образом, получился случай, когда при протекании термодинамического процесса растекания капли жидкости внутренняя энергия системы сохраняется неизменной. Аналогичный частный случай термодинамической системы подробно рассмотрен в работе [5] при адиабатическом расширении (dQ =0) определённого количества газа без совершения механической работы (dA=0). Но при этом происходило изменение термодинамических параметров (P,V) в соответствии с уравнением состояния и возрастание энтропии системы.
Рассмотрим в нашем случае изменение термодинамических параметров системы в процессе растекания капли жидкости. При растекании капли жидкости по твердой поверхности давление в системе не меняется (P=Const). И, поскольку термодинамические параметры при растекании капли жидкости сохраняются неизменными (P,V,T=Const), на графике в термодинамических координатах (V–P, V– T, P – T) процесс изображается в виде точки.
Наконец, определим изменение величины энтропии при растекании капли жидкости по твердой поверхности. Выражение для определения элементарного изменения величины энтропии имеет вид [5]:
dS = (dE + PdV)/T (6)
В рассматриваемом случае растекания капли несжимаемой жидкости по поверхности твердого тела изменения внутренней энергии системы не происходит (dE=0) и PdV=0. Получается, что при растекании капли жидкости по поверхности твердого тела энтропия системы сохраняется неизменной:
S = 0. (7)
Получается, что при переходе исследуемой системы в равновесное состояние ее внутренняя энергия сохраняется неизменной (E=Const), а не достигает минимального значения, и энтропия системы также сохраняется постоянной (S = 0), а не достигает максимального значения, как это происходит в случае термодинамического процесса перехода системы в равновесное состояние [4]. Сам же процесс растекания капли жидкости в термодинамических координатах изображается в виде точки.
Таким образом, полученные результаты вступают в противоречие с основополагающими понятиями термодинамической системы. Это позволяет сделать основной вывод о том, что трехфазную систему твердое тело / жидкость / пар не представляется возможным рассматривать в качестве термодинамической системы.
3. Обсуждение результатов
Следовательно, из двух подходов (термодинамического и механического) при оценке исследуемой системы правильным следует признать механический, т.е. исследуемая трехфазная система твердое тело / жидкость / пар является разновидностью изолированной механической системы. В изолированной механической системе между телами происходит силовое взаимодействие и обмен энергией только в механической форме (потенциальной или кинетической). Закон сохранения энергии, в общем случае перемещения тел с большими скоростями, может быть сформулирован в следующем виде: сумма потенциальной и кинетической энергий тел в изолированной системе сохраняется неизменной. В частном случае перемещения тел с небольшими скоростями сохраняется постоянной сумма их потенциальных энергий.
Как известно, механическая потенциальная энергия тела не мыслима без присущей ей консервативной силы, стремящейся уменьшить ее до минимума. Так, например, потенциальная энергия тела, поднятого над поверхностью, связана с силой притяжения к земле. Потенциальная энергия растянутой пружины связана с силой упругости. Потенциальная энергия поверхностного натяжения жидкости (воды, мыльной пленки) связана с силой поверхностного натяжения и т.д.
В процессе взаимодействия тел в изолированной механической системе основную, главную роль играет взаимодействие их сил. В том случае, когда в изолированной системе действуют несколько (две и более) консервативных сил, равновесие системы наступает, когда равнодействующая всех сил становится равной нулю. При этом в соответствии с законом сохранения энергии, сумма потенциальных энергий тел сохраняется постоянной. В этом случае происходит обмен потенциальных энергий между телами системы. Примером такой системы является система, состоящая из груза, подвешенного на пружине. При опускании груза пружина растягивается. Равновесие системы наступает, когда сила упругости пружины становится равной весу груза. При этом увеличение потенциальной энергии растянутой пружины равно уменьшению гравитационной потенциальной энергии груза.
Совсем иная картина складывается в другом случае, когда в системе действует только одна консервативная сила. При этом возможны два варианта равновесия такой системы. В первом варианте в состоянии равновесия происходит самопроизвольное обнуление консервативной силы (например, в случае растянутой пружины). Во втором – действующая в системе консервативная сила (как правило, постоянная) уравновешивается реакцией опоры. Но в любом случае в состоянии равновесия потенциальная энергия такой механической системы становится минимальной. Это позволило провести аналогию между равновесием механической системы с одной консервативной силой и равновесием двухфазной термодинамической системы [4].
В соответствии с подходом Юнга величина равновесного краевого угла определяется соотношением двух сил (адгезии и когезии), действующих на линии смачивания. Однако, если строго следовать по Юнгу, полученное уравнение [8]
Cosθ0=τ/ γЖГ, (8)
(где τ – сила адгезии, γЖГ – сила поверхностного натяжения) оказалось неопределенным (по причине неясности, как определять силу адгезии), и поэтому его невозможно было применять на практике.
Вместе с тем, из уравнения (8) следует, что в замкнутой системе твердое тело / жидкость / пар действуют несколько консервативных сил и, следовательно, имеем первый случай равновесия механической системы.
В заключение можно отметить, что уравнение (8) послужило исходной базой при выводе нового уравнения краевого угла смачивания (уравнения Юнга-Верхоломова).
Выводы
1. Показана неработоспособность классического уравнения Юнга для определения равновесного краевого угла смачивания θ0, полученного в рамках термодинамического подхода. Имеющиеся экспериментальные данные в области θ0>600 свидетельствуют, что между величинами Cosθ0 и поверхностной энергией на границе твердое тело/пар σSV отсутствует четкая однозначная зависимость: погрешность разброса экспериментальных точек доходит до 50%.
2. Получено, что изолированную трехфазную систему твердое тело / жидкость / пар следует рассматривать как разновидность механической системы, основанной на взаимодействии нескольких сил, действующих в системе. Равновесие такой системы достигается, когда равнодействующая всех сил, действующих в системе, становится равной нулю.
Литература
- Адамсон А. Физическая химия поверхностей. М.: Мир, 1979. 568 с.
- Верхоломов В.К. О работе адгезии при смачивании твердой поверх-ности жидкой фазой // Science and World. – 2017. – №4. –V.1. –С.11-14.
- Григорьев Г.А. Термодинамика и кинетика смачивания и растекания. М.: МИТXТ им. М.В. Ломоносова, 2008. 76 с.
- Гуггенгейм Е.А. Современная термодинамика, изложенная по методу У. Гиббса М.-Л.: Гостеххимиздат, 1941. 188 с.
- Планк М. Термодинамика. М.-Л.: Госиздат, 1925. 311 с.
- Русанов А.И. Термодинамика поверхностных явлений. Л.: Изд. ЛГУ, 1960. 179 с.
- Сумм Б.Д. Физико-химические основы смачивания и растекания. М. : Химия, 1976. 232 с.
- Сумм Б.Д. Гистерезис смачивания.// Соровский образовательный журнал. 1999. №7. С. 98-104.
- Fowkes F.M. Dispersion Force Contributions to Surface and Interfacial Tensions, Contact Angles, and Heats of Immersion. // Advances in Chemistry Se-ries. American Chemical Society, Washington. 1964. №43. P. 99-111.
- Owens D.K., Wendt Estimation of the Surface Free Energy of Poly-mers. // J. Appl. Polym. Sci. 1969. V.13. P. 1741-1747.
- Verkholomov V.K. Two Concepts While Determining Contact Angle Value. // Modern Science. 2017. №1. P.8-13.
- Verkholomov V.K. Physical Features of the New Equation (Equation Jung - Verkholomov) of Contact Angle. // Materials of the XII international re-search and practice conference "Science, Technology and Higher Education". De-cember 21-22, 2016. Westwood, Canada. P. 97-110.
- Жалоба
- 1 239
- syshatunov от