About the new equation of contact angle (EN) / О новом уравнении краевого угла смачивания (RU)
В. К. Верхоломов
Аннотация
Показано, что по основным физическим характеристикам систему твердое тело/жидкость/пар нельзя рассматривать, как термодинамическую. Она является разновидностью механической системы. С привлечением молекулярно-кинетической теории получено новое уравнение равновесного краевого угла смачивания следующего вида: Cosθ0 = (σA – σLS)/ σLV, где σA – сила адгезии поверхности твердого тела на границе с паром; σLS, σLV – силы поверхностного натяжения жидкости на границах раздела фаз жидкость/твердое тело и жидкость/пар соответственно. На основании экспериментальных данных получена четкая однозначная зависимость между Cosθ0 и силой адгезии σA: погрешность разброса экспериментальных точек относительно аппроксимирующей линии не превосходит 1%.
// Materials of the XI international research and practice conference "Science, Technology and Higher Education". October 19-20, 2016. Westwood, Canada. P. 138-143.
Введение
Важнейшей характеристикой в теории поверхностных явлений вообще и в процессах смачивания в частности является величина равновесного краевого угла смачивания θ0 между гладкой однородной не деформируемой поверхностью твердого тела и касательной к поверхности капли жидкости в точке на линии смачивания (линии трехфазного контакта). С помощью краевого угла θ0 в ряде случаев можно получить представление о характеристиках структуры твердой поверхности [1]. Можно судить не только о степени гидрофобности твердой поверхности, но и о том, как меняется эта степень при воздействии различных внешних факторов: например, влажности [2], температуры [3] и др. Поэтому определение величины краевого угла является важной задачей при исследовании поверхностных явлений, сопровождающих процесс смачивания.
Как известно, определение краевого равновесного угла смачивания θ0 проводится с помощью уравнения Юнга. Сам Юнг считал, что величина краевого угла определяется соотношением двух сил, действующих на линии смачивания капли жидкости, нанесенной на твердую поверхность: с одной стороны, сил притяжения молекул жидкости к твердой поверхности (силы адгезии), с другой – сил взаимного притяжения между молекулами жидкости (силы когезии) [4]. Таким образом, Юнг рассматривал систему взаимодействующих тел твердое тело / жидкость / пар, как разновидность механической системы, основанной на взаимодействии возникающих при смачивании сил. Главным условием равновесия такой системы является равенство нулю равнодействующей сил, действующих на линии смачивания.
Однако со временем в период бурного развития термодинамики возобладала и поныне монопольно господствует концепция, согласно которой такая система (твердое тело / жидкость / пар), без должных на то оснований, стала рассматриваться, как термодинамическая система. На основе термодинамической концепции было получено уравнение равновесного краевого угла смачивания.
1. Оценка корреляции между Cosθ0 и свободной поверхностной энергией твердого тела σSV
Для термодинамической системы справедливо одно из основных положений термодинамики: в состоянии равновесия потенциальная энергия системы минимальна. На основании такого термодинамического подхода было получено уравнение равновесного краевого угла смачивания, широко известного под именем уравнения Юнга
Cosθ0 = (σSV – σSL)/ σLV, (1)
где σSV – величина поверхностной энергии на межфазной границе твердое тело / пар; σSL – величина поверхностной энергии на границе твердое тело/жидкость; σLV – величина поверхностной энергии на границе жидкость / пар.
Таким образом, на основании термодинамического подхода в уравнение краевого угла вошли только величины поверхностных энергий на границах взаимодействующих фаз. При этом полностью (или частично) отрицается наличие движущих сил и сил сопротивления в процессе растекания капли по твердой поверхности. Можно отметить, что в качестве фактора, способствующего растеканию капли по поверхности твердого тела, выступает свободная поверхностная энергия σSV.
Сравнительно недавно появились работы [5-7], в которых поверхностная энергия, как твердого тела, так и жидкости были представлены в виде суммы двух составляющих: дисперсионной и полярной. С привлечением уравнения для работы адгезии это позволило, в конечном счете, определять величину поверхностной энергии различных твердых тел, твердых поверхностей.
В общем случае взаимодействия капли полярной жидкости с полярной поверхностью твердого тела, для величины поверхностной энергии на границе твердое тело/жидкость в работе [6] получено следующее выражение:
σSL = (√σSVd - √σLVd )2 + (√σSVp - √σLVp )2, (2)
где σSVd, σLVd – дисперсионные составляющие поверхностной энергии и поверхностного натяжения твердого тела и жидкости соответственно;
σSVp, σLVp – полярные составляющие поверхностной энергии и поверхностного натяжения твердого тела и жидкости соответственно.
Уравнение (2) показывает, что величина σSL зависит от составляющих поверхностной энергии, как твердого тела, так и жидкости.
В соответствии с уравнением Юнга (1), принимая также во внимание уравнение (2), краевой угол смачивания должен быть функцией поверхностных энергий твердого тела и жидкости, т. е. θ0(Cosθ0)= f(σSV, σLV). Если капли одной и той же жидкости (например, воды) нанести на различные твердые низкоэнергетические поверхности, то краевой угол должен зависеть только от поверхностной энергии на границе твердое тело / газ, т. е. θ0 = f(σSV). Для подтверждения наличия такой зависимости обратимся к экспериментальным данным.
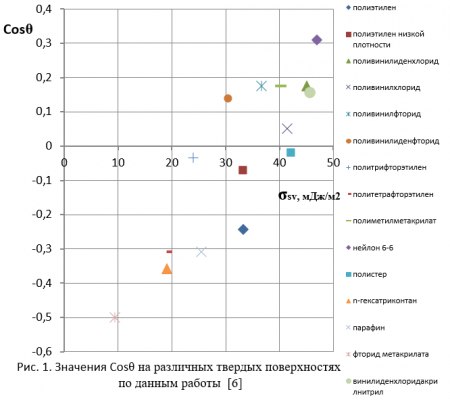
На рис. 1 приведены значения Cosθ0 (в области относительно высоких значений θ0>600), полученные на основании экспериментальных данных работы [6] при смачивании водой полимеров с различными величинами σSV. Можно отметить, что на рис. 1 представлена лишь небольшая часть имеющихся в литературе экспериментальных данных. Как следует из рис., экспериментальные точки легли с большим разбросом: погрешность разброса доходит до 50%. Это делает практически невозможным получить с приемлемой погрешностью зависимость между величинами Cosθ0 и σSV. Таким образом, можно говорить лишь о тенденции возрастания величины Cosθ0 с увеличением поверхностной энергии σSV.
Следовательно, все имеющиеся экспериментальные данные свидетельствуют о том. что между величинами Cosθ0 и σSV отсутствует четкая однозначная зависимость. Такой же вывод можно сделать по поводу корреляции θ0 и σSV. Из всего полученного следует, что классическое уравнение Юнга, полученное с помощью термодинамического подхода, не работает. Требуется его пересмотреть. Но прежде ответим на вопрос, можно ли систему твердое тело / жидкость / пар рассматривать, как термодинамическую.
2. Изолированная система взаимодействующих тел
Термодинамическая концепция для рассматриваемой системы твердое тело / жидкость / пар принята, несмотря на большие противоречия свойств системы имеющимся фактам. Главное противоречие заключается в том, для термодинамической системы обязательны термические взаимодействия, т. е. обмен энергией в форме теплоты, как с внешней средой, так и между элементами системы. Но такой обмен в рассматриваемой системе отсутствует по двум причинам. Во-первых, процесс смачивания и растекания капли жидкости по твердой поверхности рассматривается, как изолированный от воздействий со стороны окружающей среды. Во-вторых, этот процесс рассматривается, как изотермический (T=Const). Термическое взаимодействие, как известно, возникает только при наличии разности температур.
В зависимости от физических характеристик процессов взаимодействия, изолированные (замкнутые) системы могут быть разных видов: механические, термодинамические, электродинамические др. Для нас представляют интерес два вида изолированных систем: термодинамическая и механическая.
В изолированной термодинамической системе между телами происходит обмен энергией не только в механической форме, но обязательно также в форме теплоты, т. е. термического взаимодействия. Закон сохранения энергии для таких систем записывается в характерной термодинамической форме. Для описания состояния термодинамических систем вводятся термодинамические величины: теплота, внутренняя энергия, энтальпия, температура, объем, давление и т. д.
В изолированной механической системе между телами происходит силовое взаимодействие и обмен энергией только в механической форме (потенциальной или кинетической). Закон сохранения энергии, в общем случае перемещения тел с большими скоростями, может быть сформулирован в следующем виде: сумма потенциальной и кинетической энергий тел в изолированной системе сохраняется неизменной. В частном случае перемещения тел с небольшими скоростями сохраняется неизменной сумма их потенциальных энергий. Для описания состояния механических систем используются такие величины, как сила, масса, скорость, ускорение и т. д.
Поэтому представляется важным вначале определить по характеру физических процессов, к какому виду относится конкретная система взаимодействующих тел и только после этого рассматривать соответствующие уравнения сохранения. Будет неправильно, если к механической системе применять законы и положения термодинамики или к термодинамической системе применять законы механики.
Изолированную систему твердое тело / жидкость / пар, поскольку в ней не происходит обмен энергией между телами в форме теплоты, нельзя рассматривать как термодинамическую. Она является разновидностью механической системы, в которой между телами происходит силовое взаимодействие и обмен механической потенциальной энергией.
Следует подчеркнуть, что механическая потенциальная энергия тела не мыслима без присущей ей консервативной силы, стремящейся уменьшить ее до минимума. Так, например, потенциальная энергия тела, поднятого над поверхностью, связана с силой притяжения к земле. Потенциальная энергия растянутой пружины связана с силой упругости. Потенциальная энергия поверхностного натяжения жидкости (воды, мыльной пленки) связана с силой поверхностного натяжения и т.д.
В процессе взаимодействия тел в изолированной механической системе основную роль играет взаимодействие их сил. Равновесие изолированной системы наступает тогда, когда равнодействующая всех сил, действующих в системе, становится равной нулю.
3. Новое уравнение краевого угла смачивания
Получение нового уравнения краевого угла смачивания стало возможным, если систему твердое тело / жидкость / пар рассматривать, как разновидность механической системы, равновесие которой достигается при равенстве нулю равнодействующей сил, приложенных к телам системы. Новое уравнение, полученное с привлечением положений молекулярно-кинетической энергии, имеет следующий вид:
Cos θ0=(σA–σLS)/σLV , (3)
где σA – сила адгезии твердой поверхности на границе с паром; σLS, σLV – силы поверхностного натяжения жидкости на границах раздела жидкость/твердое тело и жидкость / пар соответственно.
Основное отличие нового уравнения (3) от уравнения Юнга (1) заключается в том, что вместо поверхностной энергии на межфазной границе твердое тело / пар σSV входит величина силы адгезии σA твердой поверхности, о которой еще в свое время говорил Юнг. Возникающая при смачивании сила адгезии имеет ограниченную область действия. Ее можно представить в виде площади круга, соосного с основанием капли жидкости, лежащей на твердой поверхности. Можно отметить, что уравнение (3) надежно работает в области относительно высоких значений краевого угла при θ0 > 600.
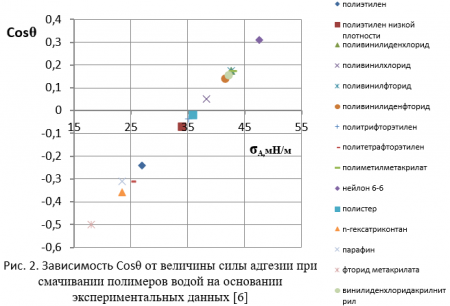
Обследование тех же экспериментальных данных, что и на рис. 1, с помощью нового уравнения (3) показало, что между Cosθ и σA существует четкая однозначная пропорциональная зависимость (рис. 2). Погрешность разброса экспериментальных точек относительно аппроксимирующей линии не превышает 1%. Следует еще раз подчеркнуть, что использовались одни и те же экспериментальные данные, что и на рис. 1. Это в ответ на возражения некоторых сторонников термодинамического подхода при определении уравнения краевого угла о причинах большого разброса экспериментальных точек по формуле Юнга (погрешность до 50%). В качестве главных причин они называют неправильное измерение краевого угла смачивания другими авторами, не учет тонких жидких пленок на твердых поверхностях при определении σSV и др.
В заключение следует отметить, что целесообразно провести специальные эксперименты по оценке размеров локальной области действия и величины силы адгезии на твердой поверхности вокруг сидящей капли жидкости (в первую очередь, воды). Это можно сделать, например, с помощью методов атомно-силовой микроскопии.
Выводы
1. Показана неработоспособность классического уравнения Юнга для определения равновесного краевого угла смачивания θ0, полученного в рамках термодинамического подхода. Имеющиеся экспериментальные данные в области θ0>600 свидетельствуют, что между Cosθ0 и поверхностной энергией на границе твердое тело / пар σSV отсутствует четкая однозначная зависимость: погрешность разброса экспериментальных точек доходит до 50%.
2. Показано, что изолированную систему твердое тело / жидкость / пар следует рассматривать, как разновидность механической системы, основанной на взаимодействии сил, действующих в системе. В рамках этой концепции получено новое уравнение краевого угла θ0, в которое вместо поверхностной энергии σSV вошла сила адгезии σA. Экспериментальные данные в области θ0>600 показали, что между Cosθ0 и σA существует однозначная пропорциональная зависимость: погрешность разброса экспериментальных точек относительно аппроксимирующей линии не превышает 1%.
3. Целесообразно провести специальные эксперименты по оценке размеров области действия и величины силы адгезии на твердой гладкой однородной поверхности вокруг сидящей капли жидкости (воды) с помощью, например, методов атомно-силовой микроскопии.
Литература
- Емельяненко А.М., Бойнович Л.Б. Анализ смачивания как эффективный метод изучения покрытий, поверхностей и происходящих на них процессов (обзор). // Заводская лаборатория. Диагностика материалов. 2010. Т.76. №9. С.27-36.
- Пашинин А.С., Емельяненко А.М., Бойнович Л.Б. Взаимодействие гидрофобных и супергидрофобных материалов с водными средами. // Физикохимия поверхности и защита материалов. 2010. Т.46. №6. С.664-670.
- Верхоломов В.К. Экспериментальная оценка гидрофобных свойств различных покрытий. // Физика и химия обработки материалов. 2014. №3. С.33-37.
- Сумм Б.Д. Гистерезис смачивания. // Соровский образовательный журнал. 1999. №7. С.98-102.
- Fowkes F.M. Dispersion Force Contributions to Surface and Interfacial Tensions, Contact Angles, and Heats of Immersion. Advances in Chemistry Series. American Chemical Society, Washington. 1964. №43. P.99-111.
- Owens D.K., Wendt R.C. Estimation of the Surface Free Energy of Polymers. // J. Appl. Polym. Sci. 1969. V.13. P. 1741-1747.
- Good R.G., van Oss C.J. in: M.E. Schrader, G. Loeb (Eds.), Modern Approaches to Wettability: Theory and Applications, Plenum Press. New York.1991. P. 1-27.
- Thorpe A.A., Peters V., Smith J.R., Thomas G., Nevell T.G. Tsibouklis Poly(methylpropenoxyfuoroalkylsiloxane)s: a class of fluoropolymers capable of inhibiting bacterial adhesion onto surfaces. // J. of Fluorine Chemistry. 2000. №104. P.37-45.
- Nishino T., Meguro M., Nakamae K., Matsushita M., Ueda Y. The Lowest Surface Free Energy Based on –CF3 Alignment. // Langmuir.1999. V.15. №13. P.4321-4323.
- Бойнович Л.Б., Емельяненко А.М. Гидрофобные материалы и покрытия: принципы создания, свойства и применение. // Успехи химии. 2008. Т.77. №7. С.619-638.
- Жалоба
- 1 086
- syshatunov от