Physical features of new equation (Young-Verkholomov equation) of contact angle of wetting (EN) / Физические особенности нового уравнения (уравнения Юнга-Верхоломова) краевого угла смачивания (RU)
В. К. Верхоломов
Аннотация
Изолированную систему твердое тело / жидкость / пар следует рассматривать, как разновидность механической системы, основанной на взаимодействии сил, действующих в системе. В рамках этой концепции и с привлечением молекулярно-кинетической теории рассмотрены силовые характеристики на границах раздела фаз при смачивании низкоэнергетических гладких твердых поверхностей. Показано, что величина силы адгезии, возникающей при смачивании между частицами (молекулами) жидкости, размещенными на линии трехфазного контакта, и частицами на поверхности твердого тела, зависит от поверхностных энергетических характеристик, как твердого тела, так и жидкости. Полученное новое уравнение (уравнение Юнга-Верхоломова) равновесного краевого угла смачивания имеет следующий вид:
Cosθ0 = (σA - σLS) / σLV,
где σA - сила адгезии на границе раздела фаз твердое тело / пар;
σLS, σLV - поверхностные натяжения жидкости на границах раздела фаз жидкость / твердое тело, жидкость / пар соответственно.
// Materials of the XII international research and practice conference "Science, Technology and Higher Education". December 21-22, 2016. Westwood, Canada. P. 97-110.
Введение
Как известно [1,2], смачивание поверхности твердого тела жидкой фазой определяется физико-химическими процессами взаимодействия, протекающими на поверхности раздела фаз, участвующих в смачивании. Процесс смачивания во многом зависит от энергетических характеристик поверхностей на границах фаз, участвующих в смачивании, и, прежде всего, от поверхностного натяжения жидкости на границе с газом σLV.
Важнейшей характеристикой процесса смачивания в системе твердое тело/жидкость/пар является величина равновесного краевого угла θ0. С помощью краевого угла можно судить не только о степени гидрофобности поверхности, но и о том, как меняется эта степень при воздействии различных внешних факторов (например, влажности, температуры и др.) [3]. В связи с этим определение величины краевого угла смачивания является важной задачей при исследовании поверхностных явлений, сопровождающих процесс смачивания.
В настоящее время определение краевого угла смачивания θ0 проводится с помощью уравнения Юнга. Юнг считал, что величина краевого угла зависит от соотношения двух сил, действующих на линии смачивания (линии трехфазного контакта) капли жидкости, нанесенной на твердую поверхность: с одной стороны, сил притяжения молекул жидкости к твердой поверхности (силы адгезии), с другой – сил взаимного притяжения между молекулами жидкости (силы когезии) [4]. Таким образом, Юнг рассматривал систему твердое тело/жидкость/пар в качестве разновидности механической системы, основанной на взаимодействии возникающих при смачивании сил.
Однако со временем возобладала и продолжает монопольно господствовать концепция, согласно которой такая система (твердое тело / жидкость / пар) рассматривается, как термодинамическая система. На основании такого термодинамического подхода было получено уравнение равновесного краевого угла, названное именем Юнга
Cosθ0=(σSV - σSL)/ σLV, (1)
В уравнение Юнга помимо энергии поверхностного натяжения жидкости (σLV), входят еще две величины: значения поверхностных энергий на границах раздела фаз твердое тело/пар (σSV) и твердое тело/жидкость (σSL). Таким образом, на основании термодинамического подхода в уравнение краевого угла вошли только величины поверхностных энергий на границах взаимодействующих фаз.
Большим достижением теории поверхностных явлений последнего времени явилось то, что свободная поверхностная энергия, как твердого тела, так и жидкости была представлена в виде суммы двух составляющих: дисперсионной и полярной [5-7]:
σSV = σSVd + σSVp (2)
σLV = σLVd + σLVp , (3)
где σSVd, σLVd – дисперсионные составляющие поверхностной энергии и поверхностного натяжения твердого тела и жидкости соответственно;
σSVp, σLVp – полярные составляющие поверхностной энергии и поверхностного натяжения твердого тела и жидкости соответственно.
Предпринятая в работе [8] попытка подтвердить, в соответствии с уравнением (1), зависимость Cosθ от поверхностной энергии на границе твердое тело/пар Cosθ=f(σSV), на основании имеющихся в литературе экспериментальных данных, окончилась неудачей. Экспериментальные точки на графике легли с большим разбросом (погрешность разброса доходила до 50%) [8]. Это позволяет сделать вывод о том, что между Cosθ и σSV отсутствует четкая однозначная зависимость, т.е. полученное на основании термодинамического подхода классическое уравнение Юнга не работает. Требуется пересмотреть уравнение краевого угла смачивания.
Такой пересмотр уравнения краевого угла стал возможным, если систему твердое тело/жидкость/пар рассматривать, как разновидность механической системы, равновесие которой достигается при равенстве нулю равнодействующей сил, действующих в системе.
Однако вначале еще раз остановимся на вопросе о том, можно ли считать систему твердое тело/жидкость/пар термодинамической системой.
1. Система твердое тело/жидкость/пар, как термодинамическая система
Примем в качестве основного допущения, что система твердое тело/жидкость/пар является термодинамической системой. Как известно, переход термодинамической системы из одного состояния в другое называется термодинамическим процессом. В нашем случае, в результате термодинамического процесса растекания капли жидкости по поверхности твердого тела система переходит из начального в конечное равновесное состояние. Всякий термодинамический процесс всегда описывается соответствующей линией на графике в термодинамических координатах (например, V–P). При осуществлении процесса происходит изменение термодинамических параметров системы, к системе из окружающей среды может подводится или отводится тепло, механическая работа, могут также происходить изменения состава системы. При этом для любого процесса перехода системы из одного состояния в другое действует закон сохранения энергии (первое начало термодинамики). В общем виде его можно записать следующим образом [9]:
dE = dQ – dA + ∑( ∂E/∂ni)s,v,njdni , (4)
где E – внутренняя энергия системы; Q – тепло, подведенное к системе из окружающей среды; A – механическая работа, отведенная от системы в окружающую среду; ni – количество молей iго компонента системы. Можно отметить, что в отличие от работы [9], где механическая работа к системе подводится и поэтому она в уравнение вошла со знаком «+», мы приняли, что в уравнении (4) механическая работа от системы отводится.
Если выразить элементарное количество тепла с помощью зависимости dQ=TdS, элементарное количество механической работы dA=PdV, и (∂E/∂ni)s,v.nj=µi, получим
dE = TdS – PdV + ∑ µi dni , (5)
где T – температура системы; S – энтропия; P – давление; V – объем; µi – химический потенциал iго компонента системы.
Итак, мы рассматриваем процесс растекания капли жидкости по поверхности твердого тела, как термодинамический процесс. При этом примем, что жидкость однокомпонентная, процесс растекания является изолированным, изотермическим (T=Const) и физическим (т.е. не происходит химических реакций, процессов растворения и т.д.).
Поскольку система является изолированной (замкнутой), подвод тепла из окружающей среды отсутствует, т.е. dQ=TdS=0. Из этого следует, что энтропия системы при растекании капли жидкости не изменяется
S = Const. (6)
Жидкость капли при давлении окружающей среды считается несжимаемой (V=Const), поэтому dV=0. Следовательно, механическая работа PdV=0. Так как жидкость является однокомпонентной и процесс растекания является физическим, то состав системы не меняется и dni=0. В итоге из уравнения (5) следует, что изменения внутренней энергии системы в процессе растекания капли жидкости по твердой поверхности не происходит dE=0, т.е.
E = Const. (7)
В процессе растекания капли жидкости давление в окружающей среде не изменяется, т.е. процесс растекания является также и изобарическим (P=Const). В термодинамических координатах объем–давление (V–P) процесс растекания капли жидкости изобразится на графике в виде точки (P=Const; V =Const). В термодинамических координатах энтропия–температура (S–T) процесс растекания капли жидкости также изобразится в виде точки. Можно показать, что в любых других термодинамических параметрах процесс тоже изображается в виде точки. Таким образом, получается, что в процессе растекания капли жидкости не происходит изменения термодинамических параметров, а внутренняя энергия, которая является также термодинамическим потенциалом системы, сохраняется неизменной, а не достигает минимального значения в состоянии равновесия, как это происходит в случае изолированной термодинамической системы [9]. Можно показать, что сохраняются неизменными и другие термодинамические потенциалы: энтальпия H, свободная энергия Гельмгольца F и энергия Гиббса G.
Такие противоречивые результаты получились в результате принятого допущения о том, что система твердое тело/жидкость/пар является термодинамической системой. Следовательно, такую систему нельзя считать термодинамической. Следует согласиться с мнением Юнга и считать рассматриваемую систему, как разновидность механической системы.
Новое уравнение равновесного краевого угла было получено с привлечением молекулярно-кинетической теории. В рамках настоящей статьи рассмотрен частный случай физического смачивания низкоэнергетических гладких однородных твердых поверхностей однокомпонентными жидкостями. Вначале рассмотрим поверхностное натяжение жидкости на границе с паром σLV.
2. Поверхностное натяжение на границе фаз жидкость/пар
Процесс физического смачивания и растекания, как и величина равновесного краевого угла, определяются соотношением сил притяжения молекул жидкости к поверхности твердого тела (силы адгезии) и сил взаимного притяжения между частицами (молекулами) жидкости (силы когезии). Следует подчеркнуть, что эта фундаментальная характеристика процесса смачивания, являющаяся базовым положением теории Юнга, является основой проведенного в настоящей работе анализа. Силы притяжения между молекулами жидкости особенно ярко проявляются на поверхности ее раздела с газом. С большой долей вероятности можно представить следующую картину сил, действующих на поверхности жидкости. На отдельную молекулу (примем для простоты, что она имеет шаровидную форму), оказавшуюся на поверхности жидкости (на рис. 1 она зачернена), со стороны других ближайших молекул, находящихся в жидкости в пределах ее сферы молекулярного действия, действуют силы притяжения, равнодействующая которых F1 направлена вглубь жидкости (на рис. вниз) перпендикулярно к поверхности.
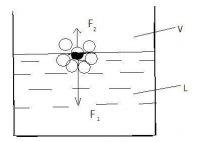
Рис. 1. Схема сил, действующих на поверхностную молекулу жидкости: L - жидкость; V - пар
Величина этой силы растет в направлении от внутренней к наружной границе поверхностного слоя. Переход молекулы из глубины жидкости в поверхностный слой сопряжен с затратой работы против действующей в поверхностном слое силы притяжения [12]. Толщина поверхностного слоя жидкости составляет примерно 10Ǻ (для воды она равна примерно трем диаметрам молекулы) [13]. Поскольку над поверхностью жидкости существует давление насыщенных паров молекул той же жидкости, то со стороны этих молекул на нашу поверхностную молекулу будут действовать силы притяжения, равнодействующая которых F2 направлена вверх. Поскольку при небольших давлениях насыщенного пара выполняется условие F1>> F2, то под действием силы F1 молекула будет втянута внутрь жидкости. Таким образом, на поверхности жидкости каждое мгновение бесчисленное множество молекул втягиваются внутрь жидкости, и на смену им такое же количество молекул выталкиваются на поверхность. Работа сил притяжения, действующих на поверхностные молекулы жидкости, приводит к возникновению поверхностного натяжения на границе раздела фаз жидкость/пар σLV.
Образно выражаясь, поверхностное натяжение жидкости характеризуется непрерывной сменой («толчеей») гигантского количества поверхностных молекул. По мере повышения температуры жидкости, во-первых, все большее количество молекул вылетает из жидкости, благодаря чему растет давление насыщенного пара, а, во-вторых, ослабляются силы притяжения между молекулами внутри жидкости. Вылетевшие из жидкости молекулы пара притягивают к себе поверхностные молекулы. Благодаря этому, сила F2 возрастает, а сила F1 уменьшается, и, как следствие, поверхностное натяжение σLV уменьшается.
Наконец, при температуре в критической точке (Ткр), по-видимому, наступает равенство F1≈ F2. При этом исчезает разница между жидкостью и паром, а поверхностное натяжение становится равным нулю.
3. Поверхностное натяжение на границе фаз твердое тело/жидкость
Рассмотрим, что происходит с молекулами жидкости на границе раздела фаз твердое тело/жидкость. На молекулу жидкости, находящуюся на границе раздела фаз, также действуют силы притяжения. С одной стороны, логично предположить, что на поверхностную молекулу действуют силы притяжения со стороны окружающих ее молекул внутри жидкости, которые стараются втянуть молекулу внутрь жидкости (ранее равнодействующую этих сил когезии мы обозначили F1). С другой стороны, на поверхностную молекулу действуют силы притяжения со стороны окружающих ее частиц (молекул, атомов) на поверхности твердого тела. Равнодействующая этих сил будет равна силе адгезии FA (рис. 2).
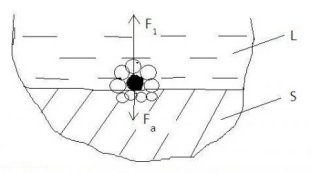
Рис. 2. Схема сил, действующих на молекулу жидкости, размещенную на поверхности твердого тела: L - жидкость; S - твердое тело
Здесь просматривается вполне определенная аналогия между силой адгезии и рассмотренной ранее силой F2: сила FA так же уменьшает поверхностное натяжение жидкости на границе раздела фаз. Таким образом, получается следующая картина. В том случае, когда сила адгезии равна нулю (FA=0), поверхностное натяжение на межфазной границе твердое тело/жидкость будет близко к σLV (σSL≈σLV), и на поверхности жидкости происходит процесс непрерывной смены молекул аналогично поверхности раздела фаз жидкость/пар. В другом предельном случае, когда сила адгезии становится равной или превышает силу когезии FA ≥ F1, поверхностные молекулы жидкости на границе фаз будут, по-видимому, жестко притянуты к поверхности твердого тела. В этом случае в соответствии с физикой явления σSL≈ 0. Поскольку речь идет о поверхностном натяжении жидкости на границе с твердым телом, целесообразно поменять нижний индекс и принять σLS (по аналогии с σLV). Таким образом, поверхностное натяжение жидкости на границе с твердым телом изменяется в следующих пределах: 0 ≤ σLS ≤σLV.
4. Новое уравнение краевого угла смачивания и обсуждение результатов
Если каплю жидкости поместить на гладкую ровную однородную поверхность твердого тела, то начинается процесс ее растекания, т.е. перемещение ее линии смачивания и увеличение площади контакта с твердой поверхностью.
В уравнении Юнга факторами сопротивления, которые тормозят растекание капли, выступают поверхностные энергии σLV и σSL, а фактором растекания капли является поверхностная энергия твердого тела на границе с газом σSV.
Но поверхностная энергия σSV в уравнении (1) относится только к твердому телу и никак не зависит от поверхностных энергетических характеристик смачивающей жидкости.
В отличие от уравнения (1), примем, что вместо поверхностной энергии σSV выступает движущая сила растекания σA - сила адгезии, введенная еще Юнгом. Как уже указывалось [8], сила адгезии, в отличие от свободной поверхностной энергии, возникает локально в месте контакта капли жидкости с твердой поверхностью. Область действия силы адгезии можно представить в виде площади круга, соосного с основанием капли жидкости, но бoльшего по размерам. На рис. 3 цифрами 1,2,3 обозначены: сила адгезии на границе твердое тело/пар, силы поверхностного натяжения жидкости на границах жидкость/пар и жидкость/твердое тело соответственно.
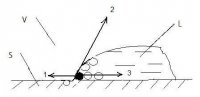
Рис. 3. Схема сил, действующих на линии смачивания капли жидкости: S - твердое тело; V - пар; L - жидкость; 1 - сила адгезии на границе твердое тело/пар; 2 - поверхностное натяжение на границе жидкость / пар; 3 - поверхностное натяжение на границе жидкость / твердое тело
Здесь уместно напомнить о содержащемся в [14] важном выводе: энергия поверхностного натяжения жидкости эквивалентна силе поверхностного натяжения. Таким образом, если речь идет о единице длины линии смачивания, то имеет место сила поверхностного натяжения, если – о единице площади поверхности жидкости, то – энергия поверхностного натяжения.
Логично предположить, что такое же эквивалентное соотношение существует между силой адгезии и поверхностной энергией адгезии, которые возникают локально в месте контакта капли жидкости с твердой поверхностью.
С учетом сказанного выше, новое уравнение равновесного краевого угла принимает следующий вид:
Cosθ0 = (σA - σLS) / σLV, (8)
где σA – сила адгезии на границе твердое тело/пар; σLS, σLV –поверхностные натяжения жидкости на границах раздела жидкость/твердое тело и жидкость/пар соответственно. Чтобы отличить уравнение (8) от классического уравнения Юнга (1), новое уравнение краевого угла смачивания назовём уравнением Юнга-Верхоломова.
Рассмотрим более подробно величину поверхностного натяжения жидкости на границе раздела фаз жидкость/твердое тело σLS, которое, как уже сказано, является результатом действия на поверхностные молекулы жидкости сил когезии, с одной стороны, и сил адгезии, с другой. Результатом действия сил когезии на поверхности жидкости (в случае, когда давление насыщенного пара близко к нулю) является поверхностное натяжение жидкости, которое обозначим σL0, а результатом действия сил адгезии - σA0 (по аналогии с σS0 на границе твердое тело/вакуум из [11]). Поскольку силы σL0 и σA0 разно направлены, получим следующее выражение для σLS:
σLS = σL0 - σA0, (9)
В частном, но важном для практики случае, когда давление насыщенного пара мало, можно принять, что величины поверхностного натяжения жидкости σL0 и σLV достаточно близки, т.е. σL0≈σLV. Примем также в качестве допущения, что σA0≈σA. Тогда выражение (9) принимает следующий вид:
σLS ≈ σLV - σA. (91)
Подставляя (91) в (8), получим приближенное новое уравнение для равновесного краевого угла
Cosθ0 ≈ (2σA - σLV) / σLV. (81)
Как известно, уравнение равновесного краевого угла через работу адгезии (уравнение Юнга-Дюпре) имеет вид [14]
Cosθ0 = (WA - σLV) / σLV. (10)
Приравнивая правые части уравнений (81,10), получаем следующие уравнения:
WA ≈ 2σA, (11)
σA ≈ WA / 2 . (12)
В работе [5] было получено следующее уравнение для работы адгезии, удовлетворительно согласующееся с экспериментальными данными:
WA = (1 + Cosθ0) σLV = 2(√σSVd σLVd + √σSVp σLVp ), (13)
где σSVd, σLVd – дисперсионные составляющие поверхностной энергии и поверхностного натяжения на границе фаз твердое тело/пар и жидкость/пар соответственно,
σSVp, σLVp – полярные составляющие поверхностной энергии и поверхностного натяжения на границе фаз твердое тело/пар и жидкость/пар соответственно.
Из уравнений (12,13) получаем приближенное выражение для определения величины силы адгезии на границе твердое тело/пар
σA ≈√σSVd σLVd + √σSVp σLVp (14)
Из уравнения (14) следует, что в величину силы адгезии на равных основаниях входят полярные и дисперсионные составляющие, как свободной поверхностной энергии твердого тела, так и поверхностного натяжения жидкости.
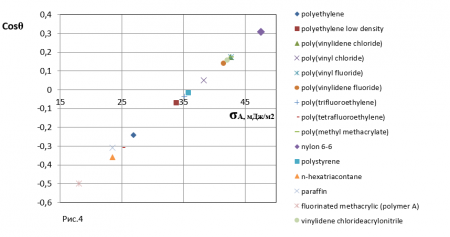
В отличие от величины поверхностной энергии, которая для каждого твердого тела (твердого покрытия) является постоянной, сила адгезии (поверхностная энергия адгезии) для данного твердого тела является величиной переменной при взаимодействии с разными жидкостями. В общем случае, в соответствии с уравнениями (8,9), краевой угол также должен быть в функциональной зависимости от σA, σLV, σL0, σA0, т.е. θ=f(σA, σLV, σL0, σA0). В частном случае, когда можно приближенно принять σL0≈σLV, σA0≈σA, θ≈f(σA, σLV), и при использовании одной и той же жидкости (например, воды) имеем θ≈f(σA). На рис. 4 приведены значения Cosθ0, полученные на основании экспериментальных данных работы [6] при смачивании водой нескольких полимеров, различающихся величинами σA. Получена четкая однозначная пропорциональная зависимость Cosθ0≈f(σA). Для случая воды, с погрешностью ~ 1%, она может быть аппроксимирована уравнением
Cosθ0=0,0269σA – 0,976 (15)
Таким образом, установлено, что величина возникающей при смачивании силы адгезии зависит от поверхностных энергетических характеристик, как твердого тела, так и смачивающей жидкости.
Можно также отметить, что, в отличие от уравнения энергетического баланса (10), уравнения (8,81) можно рассматривать и как уравнения энергетического баланса, и как уравнения баланса сил. Таким образом, получается, что уравнение Юнга-Дюпре является частным случаем уравнения Юнга-Верхоломова.
Необходимо обратить внимание на важное утверждение, содержащееся в [14], о том, что «…во все уравнения, описывающие трехфазную границу, σSV и σSL всегда (подчеркнуто автором статьи) входят в виде разности… (адгезионного натяжения)». А разность этих величин вполне правомерна, так как она равна проекции величины поверхностного натяжения жидкости на горизонтальную ось: σLVCosθ0. Более того, получается, что обе разности, входящие в уравнения (1) и (8), равны между собой
σSV - σSL = σA - σLS. (16)
При этом между σSV и σA с одной стороны и между σSL и σLS с другой, существует значительная разница. Например, для исследованного в работе [10] перфторэйкозана C20F42 σSV=6,7 мДж/м2, а σA=18,7 мДж/м2).
Главным отличием предложенной концепции является то, что движущей силой при растекании капли является возникающая сила адгезия, а не поверхностная энергия твердого тела. Это еще раз убедительно подтверждает, что систему твердое тело/жидкость/пар следует рассматривать, как разновидность механической системы.
Другое отличие заключается в том, что вместо физически непонятной величины поверхностной энергии на межфазной границе твердое тело/жидкость σSL в уравнение Юнга-Верхоломова входит величина поверхностного натяжения на границе фаз жидкость/твердое тело. Здесь просматривается аналогия между состоянием поверхностной молекулы жидкости на границе жидкость/пар и состоянием жидкостной поверхностной молекулы на границе жидкость/твердое тело.
Наконец, переход в уравнении краевого угла от поверхностной энергии σSV к силе адгезии σA имеет также значительный практический интерес, так как позволяет определить основной тренд повышения краевых углов (гидрофобных свойств) вновь разрабатываемых гладких твердых покрытий. Все имеющиеся экспериментальные данные показывают, что для повышения величин краевого угла гладких твердых покрытий при смачивании жидкостью необходимо снижать величину соответствующей силы адгезии, а не σSV.
В заключение необходимо отметить следующий момент. В работе [8] сказано, что уравнения (8,81,15) надежно работают в области значений краевого угла θ0>600. Это утверждение основано на том, что мы располагали систематизированными экспериментальными данными, соответствующими области углов θ0>600. Одиночные экспериментальные результаты показывают, что новые уравнения работают и при малых углах смачивания (θ0≈270). Однако применение уравнений при малых краевых углах смачивания требует экспериментального подтверждения.
Заключение
1. Показано, что с позиций первого начала термодинамики систему твердое тело/жидкость/пар нельзя рассматривать, как термодинамическую. Она является разновидностью механической системы.
2. Полученое уравнение Юнга-Верхоломова для равновесного краевого угла смачивания имеет следующий вид:
Cosθ0 = (σA - σLS) / σLV, где σA – сила адгезии на межфазной поверхности твердое тело/пар; σLS, σLV – поверхностные натяжения жидкости на границе раздела фаз жидкость/твердое тело и жидкость/пар соответственно.
3. Показано, что величина локально возникающей в процессе смачивания силы адгезии σA зависит от поверхностных энергетических характеристик, как твердого тела, так и жидкости.
4. Для повышения гидрофобных свойств (краевого угла θ0) вновь разрабатываемых гладких твердых поверхностей (покрытий) при смачивании той или иной жидкостью необходимо снижать величину соответствующей силы адгезии.
Литература
- Сумм Б.Д., Горюнов Ю.В. Физико-химические основы смачивания и растекания. М.: Химия, 1976. 232 с.
- Григорьев Г.А. Термодинамика и кинетика смачивания и растекания. М.: МИТXТ им. М.В. Ломоносова, 2008. 76 с.
- Верхоломов В.К. Экспериментальная оценка гидрофобных свойств различных покрытий. // Физика и химия обработки материалов. 2014. №3. С. 33-37.
- Сумм Б.Д. Гистерезис смачивания. // Соровский образовательный журнал. 1999. №7. С. 98-102.
- Fowkes F.M. Dispersion Force Contributions to Surface and Interfacial Tensions, Contact Angles, and Heats of Immersion. Advances in Chemistry Series. American Chemical Society, Washington. 1964. №43. P. 99-111.
- Owens D.K., Wendt R.C. Estimation of the Surface Free Energy of Polymers. // J. Appl. Polym. Sci. 1969. V. 13. P. 1741-1747.
- Good R.G., van Oss C.J. in: M.E. Schrader, G. Loeb (Eds.), Modern Approaches to Wettability: Theory and Applications, Plenum Press. New York.1991. P. 1-27.
- Verkholomov, V.K. About the New Equation of Contact Angle. / V.K. Verkholomov // Materials of the XI international research and practice conference "Science, Technology and Higher Education". - October 19-20, 2016. - Westwood, Canada. - P. 138-143.
- Гуггенгейм Е.А. Современная термодинамика, изложенная по методу У.Гиббса. М.-Л.: Гостеххимиздат, 1941. 188 с.
- Nishino T., Meguro M., Nakamae K., Matsushita M., Ueda Y. The Lowest Surface Free Energy Based on –CF3 Alignment. // Langmuir. 1999. V. 15. №13. P. 4321-4323.
- Жалоба
- 1 333
- syshatunov от