На основании анализа экспериментальных данных, полученных П. Л. Капицей по сверхтекучести гелия II, открыт частный случай пограничной сверхтекучести на межфазной поверхности гелий I / гелий II.

Сверхтекучестью называется способность вещества в особом состоянии (квантовой жидкости), возникающем при температурах, близких к абсолютному нулю, протекать через узкие щели и капилляры без трения [2]. Это явление впервые было открыто в 1938 г. П. Л. Капицей и Дж. Алленом. Таким образом, сверхтекучесть может проявляться только при особо низких температурах. Поскольку обладающий сверхтекучестью гелий II (He II) появляется при температурах ниже λ-точки (Т = 2,172 ºK), в настоящее время считается, что явление сверхтекучести возникает только вблизи абсолютного нуля температуры. При температурах T>2,172 ºK гелий существует только в виде нормальной однородной жидкости гелия I (He I), которая обладает обычными свойствами, присущими жидкостям, в частности вязкостью. Течение He I в каналах сопровождается возникновением сил трения на стенках, а, следовательно, потерями кинетической энергии его струи. Но при температурах ниже λ-точки (Т = 2,172 ºK) гелий I переходит в гелий II (He II). На самом деле ниже λ-точки гелий представляет смесь двух жидкостей: нормальной жидкости He I и квантовой жидкости He II, которой присущи необычные теплофизические свойства. Это, во-первых, свойство оставаться в жидком состоянии вплоть до абсолютного нуля температуры. Это, во-вторых, свойство сверхтеплопроводности (коэффициент теплопроводности у He II более чем в 200 раз выше, чем у такого теплопроводного вещества, как медь). И это, в-третьих, свойство сверхтекучести, т. е. протекать без трения через узкие щели и капилляры [3].

Поскольку переход He I в He II при температурах ниже λ-точки является фазовым переходом II рода, то по мере снижения абсолютной температуры концентрация в смеси He II возрастает, а концентрация He I уменьшается. Таким образом, из имеющихся материалов следует, что явление сверхтекучести возникает, во-первых, при температурах, близких к абсолютному нулю температур, и, во-вторых, не у любой жидкости, а только у квантовой. Поскольку сверхтекучесть имеет большое научное значение, попытаемся еще раз рассмотреть и проанализировать эксперименты П. Л. Капицы по сверхтекучести He II.

Целями настоящей работы был углубленный анализ известных экспериментов П. Л. Капицы по сверхтекучести He II.

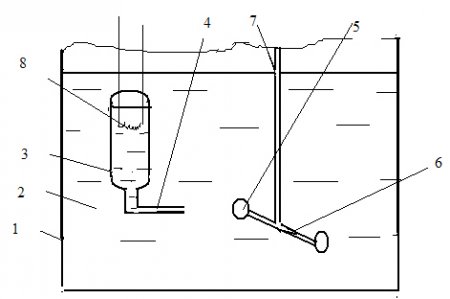
Рис. 1. Схема лабораторной установки П. Л. Капицы: 1 – сосуд Дьюара; 2 – жидкий He II; 3 – колбочка; 4 – Г-образный капилляр; 5 – лепесток; 6 – коромысло; 7 – стеклянная палочка; 8 – нить накаливания

Из всех экспериментов П. Л. Капицы по сверхтекучести подробно остановимся на эксперименте с колбочкой (бульбочкой, как ее называл Капица). На рис. 1 приведена принципиальная схема лабораторной установки (подробное описание дано в [2]). В сосуд Дьюара (1) наливается жидкий He II (2). В жидкости размещается стеклянная колбочка (3), соединенная внизу с Г-образным капилляром (4), горизонтальный выход из которого имел форму узкой щели. Напротив этой щели по ее оси располагался лепесток (5), размещенный на конце горизонтального коромысла (6). К коромыслу была припаяна стеклянная вертикальная палочка (7), которая подвешивалась на кварцевой нити. В колбочке (3) размещалась нить накаливания (8). При подаче питания на нить накаливания (8) из капиллярной щели вытекала струя, которая ударялась в лепесток (5). Сила давления на лепесток определялась по углу закручивания кварцевой нити. Парадокс опыта заключался в том, что, во-первых, уровень жидкого гелия в колбочке (3) при истечении струи оставался неизменным. А, во-вторых, даже на разных удалениях лепестка (5) от выхода щели капилляра (4) сила давления струи на лепесток не изменялась.

Этот и другие эксперименты, которые подробно описаны в [2], позволили Капице создать двухжидкостную модель течения гелия в опыте. Уровень жидкого гелия в колбочке сохранялся постоянным. И причина этого явления заключалась в том, что по стенкам щелевого отверстия капилляра (4) в колбочку непрерывно поступал сверхтекучий компонент He II. Этот компонент, отрываясь от стенок колбочки при приближении к нити накаливания (8), нагревался от нити накаливания и превращался в нормальную жидкость He I, которая вытекала из щели капилляра по центру. В результате экспериментов практически было установлено отсутствие вязкости, а, следовательно, и сил трения у He II (в экспериментах его вязкость в миллион раз была меньше, чем у He I). Таким образом, было установлено, что квантовая компонента He II обладает сверхтекучестью.

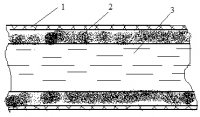
Рис. 2. Течение гелия II в капиллярной щели: 1 – стенка капиллярной щели; 2 – гелий II; 3 – гелий I

Рассмотрим еще раз течение He II в узкой капиллярной щели. На рис. 2 картина течения изображена в большом масштабе. Вдоль стенок капиллярной щели (1) течет квантовая сверхтекучая жидкость – He II (2). По центру щели течет нормальная жидкость – He I (3). Обе струи текут в противоположных направлениях: струя He I вытекает из колбочки, а струя He II втекает. При этом система не испытывает трения. Здесь можно выделить две поверхности, две границы раздела фаз. Одна поверхность между твердой стенкой щели и квантовой жидкостью He II, другая поверхность между квантовой жидкостью He II и нормальной жидкостью He I. Силы трения отсутствуют как на первой поверхности, так и на второй. Силы трения возникают, как результат сил взаимодействия между смежными фазами. Так, например, при течении воды вдоль лиофильной твердой поверхности действуют силы адгезии (между частицами твердой поверхности и молекулами воды) и силы когезии (между молекулами воды). Вследствие действия этих сил молекулы воды, прилежащие к твердой поверхности, прилипают к ней, что приводит к возникновению пограничного слоя, в котором, благодаря силам трения, происходит торможение частиц воды. При этом часть кинетической энергии переходит в тепло, т. е. происходит диссипация энергии.

Как известно [4-6], в рамках молекулярной теории смачивания удельная свободная поверхностная энергия на границе раздела фаз представляет сумму дисперсионной и полярной составляющих. Поскольку из условия сверхтекучести между стенкой щели и струей He II нет сил взаимодействия, то силы адгезии равны нулю. Из уравнения сил адгезии получаем [7]

σA = √‎σ_SV^d σ_LV^d + √‎σ_SV^p σ_LV^p = 0. (1)

где σ_SV^d, σ_LV^d – дисперсионные составляющие поверхностной энергии и поверхностного натяжения твердой стенки и жидкости He II соответственно; σ_SV^p, σ_LV^p – полярные составляющие поверхностной энергии и поверхностного натяжения твердой стенки и жидкости He II соответственно.

Но поверхностные энергетические характеристики стеклянной стенки щели отличны от нуля: σ_SV^d ≠ 0; σ_SV^p ≠ 0. В таком случае из уравнения (1) следует, что σ_LV^d = 0; σ_LV^p = 0. Из этого можно сделать вывод, что энергия поверхностного натяжения и, следовательно, силы поверхностного натяжения квантовой жидкости He II равны нулю

σ_LV = σ_LV^d + σ_LV^p = 0. (2)

А так как силы когезии между молекулами He II, по крайней мере, пропорциональны силам поверхностного натяжения, то и силы когезии в квантовой жидкости He II равны нулю. Таким образом, подтверждается ранее полученный вывод о том, что между молекулами He II отсутствуют силы притяжения [3].

Поверхность раздела между квантовой жидкостью He II и нормальной жидкостью He I можно рассматривать, как течение He I вдоль жидкой стенки He II. Из уравнения (1), записанного для этого случая, следует, что силы адгезии также равны нулю (как следует из (2), дисперсионная и полярная составляющие поверхностной энергии жидкой стенки равны нулю): σ_A = 0. Поэтому пограничный слой не образуется, и силы трения отсутствуют. Кроме того, следует отметить, что межфазная поверхность является гладкой.

Хотелось бы также сказать несколько слов по поводу следующего интересного факта, полученного в эксперименте. Как известно [1], при истечении струи обычной жидкости в неподвижную среду той же жидкости (затопленной струи) возникает струйный пограничный слой и происходит расширение струи. И, если по оси струи размещать один и тот же чувствительный лепесток, то сила давления струи на него будет ослабевать по мере удаления от среза сопла. Однако такого явления, как уже отмечено выше, в опыте с гелием не происходит: сила давления на лепесток даже при относительно большом удалении оставалась неизменной. Это можно объяснить, видимо, тем, что вокруг вытекающей струи He I на всем ее протяжении также образуется защитный слой He II, который экранирует ее. Течение слоя He II будет в сторону выходного сечения капилляра.

Таким образом, можно сделать важный вывод о том, что на поверхности раздела между квантовой жидкостью He II и нормальной жидкостью He I также возникает явление сверхтекучести, т. е. течение без потерь кинетической энергии струи на преодоление сил сопротивления в условиях отсутствия пограничного слоя. В отличие от объемной сверхтекучести квантовой жидкости He II мы имеем случай возникновения сверхтекучести только на границе раздела фаз He I и He II. Следовательно, в данном случае можно говорить о локальной или пограничной сверхтекучести нормальной жидкости He I.

Исходя из проведенного анализа, можно сформулировать следующее условие для возникновения пограничной сверхтекучести нормальной жидкости He I: на межфазной границе отсутствуют силы взаимодействия между фазами (силы адгезии).

Из анализа экспериментальных результатов П. Л. Капицы по сверхтекучести гелия II открыт частный случай пограничной сверхтекучести на межфазной границе гелий I / гелий II.