Experimental evaluation of the influence of the end effects of a capillary tube on the magnitude of the adhesion force at wetting (EN) / Экспериментальная оценка влияния концевых эффектов капиллярной трубки на величину силы адгезии при смачивании
Аннотация
Впервые получены экспериментальные результаты по силам адгезии, возникающим при растекании жидкости по твердой поверхности. С помощью разработанной в работе методики получено распределение силы адгезии по высоте области ее действия в капилляре. Показано, что 80 – 90% суммарной силы адгезии формируется в непосредственной близости от линии смачивания столба жидкости.
// Science and World. 2018. № 3, V. 1, p. 11-16
Введение
В рамках новой концепции [2] оценки системы твердое тело/жидкость/пар при смачивании, как разновидности механической системы, было получено новое уравнение Юнга-Верхоломова равновесного краевого угла смачивания следующего вида [5,6]:
Cosθ0= (σA - σLS)/σLV, (1)
где σA – сила адгезии на границе раздела фаз твердое тело/пар; σLS – сила поверхностного натяжения на границе раздела жидкость/твердое тело; σLV – сила поверхностного натяжения на границе раздела жидкость/пар.
Следует особо подчеркнуть, что новое уравнение (1) полностью согласуется с механическим подходом Юнга оценки краевого угла смачивания, изложенным в разделе VII «Когезионное притяжение твердых тел и жидкостей» работы [7].
Главные отличия нового уравнения от широко известного уравнения Юнга краевого угла смачивания состоят в следующем. Во-первых, новое уравнение является, прежде всего, уравнением баланса сил, возникающих в системе твердое тело/жидкость/пар. Во-вторых, вместо свободной поверхностной энергии твердого тела σSV вошла величина силы адгезии твердой поверхности σA. В-третьих, вместо величины поверхностной энергии на границе твердое тело/жидкость σSL в новое уравнение вошла сила поверхностного натяжения жидкости на границе раздела жидкость/твердое тело σLS. Как уже отмечалось в работе [3], здесь просматривается аналогия между состоянием поверхностной молекулы жидкости на границе жидкость/пар и состоянием поверхностной молекулы жидкости на границе жидкость/твердое тело.
Следует еще раз подчеркнуть, что определение краевого угла смачивания является фундаментальной проблемой теории смачивания.
Явление смачивания наиболее наглядно проявляется в двух случаях: при растекании капли жидкости по твердой гладкой однородной гидрофильной поверхности и при поднятии жидкости в капиллярной трубке (капиллярном поднятии).
В первом случае капля равномерно растекается во все стороны по твердой поверхности. После окончания растекания, т.е. при наступлении равновесного состояния, капля жидкости на виде сверху представляет площадь круга, радиус которого зависит от степени гидрофильности поверхности, т.е. от краевого угла. Поскольку растекание происходит по горизонтальной твердой поверхности, мы имеем дело с двумерным случаем растекания жидкости, т.е. жидкость одновременно растекается в двух направлениях: и по оси X, и по оси Y в декартовой системе координат.
Во втором случае жидкость поднимается (растекается) в одном направлении вдоль оси капиллярной трубки. Таким образом, в этом случае мы имеем дело с одномерным течением жидкости под действием возникающих в системе сил: силы адгезии поверхности стенки капилляра, силы поверхностного натяжения жидкости и силы тяжести.
Напомним, что в работе [4] было получено новое универсальное уравнение капиллярного давления, связывающее высоту поднятия жидкости в капилляре h с величиной силы адгезии поверхности капилляра σA. Если опускать капиллярную трубку в жидкость, налитую в сосуд, то высота столба жидкости в капилляре будет сохраняться неизменной до тех пор, пока не начнут действовать концевые эффекты капиллярной трубки. При этом мениск столба жидкости в капилляре начинает приближаться к торцу трубки, что приведет к сокращению площади поверхности капилляра между мениском и торцом трубки, на которой действуют силы адгезии, т.е., в конечном счете, это должно привести к уменьшению суммарной силы адгезии σA. В свете сказанного, предоставляется возможность оценить величину переменной силы адгезии (переменной высоты столба жидкости в капилляре) в зависимости от расстояния между торцом капиллярной трубки и мениском столба жидкости.
Целью настоящей работы была оценка влияния концевых эффектов капиллярной трубки на величину силы адгезии поверхности капилляра.
1. Лабораторная установка. Методики проведения экспериментов и обработки экспериментальных данных
1.1 Устройство лабораторной установки.
Лабораторная установка включала следующие элементы: лабораторный штатив, сменные капиллярные трубки, пластмассовую цилиндрическую проставку. мерный стакан или мензурку, в которые наливалась дистиллированная вода. На рис. 1 приведено фото собранной установки. На вертикальной штанге штатива размещались цилиндрическая проставка и муфта с винтами. Муфта снабжена двумя отверстиями для возможности перемещения по вертикальной штанге и для размещения горизонтального стержня. Из медной проволоки были изготовлены специальные подвески, которыми оснащалась каждая капиллярная трубка. К кольцам подвесок крепилась ниточная петля (см. рис.), с помощью которой исследуемая трубка подвешивалась в вертикальном положении на горизонтальном стержне. Принятая конструкция позволяла легко удерживать трубку в вертикальном положении. Опускание/поднятие трубки в воду осуществлялось с помощью перемещения муфты вдоль вертикальной штанги с использованием двух сменных шайб (высотой 12 и 15 мм), а также набора пластмассовых прокладок толщиной ~ 1мм.
Рис. 1 Фото лабораторной установки при проведении экспериментов
1.2 Методика проведения экспериментов
Эксперименты проводились на четырех капиллярных трубках, которые отличались размерами капилляров и длиной (табл. 1)
Таблица 1.
Характеристики капиллярных трубок
| № | Радиус капилляра r, мм | Длина трубки l, мм | Наружный диаметр трубки, мм |
| 1 | 0,6 | 100 | 7 |
| 2 | 0,6 | 100 | 7 |
| 3 | 0,7 | 165 | 5 |
| 4 | 0,7 | 165 | 5 |
Перед проведением экспериментов каналы трубок были обезжирены с помощью ватных тампонов, смоченных авиационным бензином Б-70. Предварительные эксперименты выявили трудности достоверного отсчета положения на поверхности трубки уровня воды в сосуде из-за бликов на возникающем мениске. Для исключения этого наружная поверхность каждой трубки покрывалась прозрачной полипропиленовой пленкой (с краевым углом смачивания для воды θ0≈1000). Перед этим на поверхности трубок №1 и №2 были нанесены шкалы отсчета (трубки №3 и №4 имели фабричные шкалы от 0 до 90 мм вплоть до верхнего торца). Кроме того, для большей контрастности и облегчения отсчета показаний, вода в стакане (мензурке) была подкрашена. Отсчет положений мениска в капилляре и уровня воды в широком сосуде проводились с помощью лупы (x6). Использовалась также специальная боковая подсветка.
1.3 Методика обработки экспериментальных данных
Номинальная высота поднятия жидкости (воды) составляла: для трубок №1 и №2 hN≈12мм, для трубок №3 и №4 hN≈10мм. Как было показано в работе [3], в равновесном состоянии сидящей на твердой поверхности капли площадь области действия внешней силы адгезии равна площади основания (круга) сидящей капли, т.е. ωA = ωLS. При этом в состоянии равновесия проекция силы поверхностного натяжения жидкости на горизонтальную плоскость становится равной адгезионному натяжению (поскольку в этом случае действующая на каплю сила тяжести уравновешивается реакцией твердой поверхности)
σLV Cosθ0 = (σA - σLS) (2)
В случае поднятия жидкости в капилляре картина действующих сил кардинально меняется: в равновесном состоянии сила адгезионного натяжения (σA – σLS), действующая по всей длине линии смачивания, становится равной весу столба жидкости в капилляре
(σA – σLS) 2πr = hΔρgπr2 , (3)
где r – радиус капилляра; Δρ = ρL – ρV (разность плотностей жидкой и газовой фаз); g – ускорение свободного падения; h – высота столба жидкости.
Получается, что в рассматриваемом случае имеет место другая физическая картина, когда сила поверхностного натяжения (в проекции на ось капилляра), действующая по касательной к мениску на линии смачивания, по существу не участвует в схеме действующих сил, а только играет роль эквивалента (регистратора) адгезионного натяжения.
Таким образом, было принято, что аналогом капли на горизонтальной твердой поверхности в случае капилляра является высота поднятия жидкости в капилляре, т.е. высота столба жидкости h. По аналогии с каплей на горизонтальной поверхности, будем считать, что в равновесном состоянии область действия внешней силы адгезии равна площади основания капли, т.е. в нашем случае площади цилиндрической поверхности столба жидкости. А поскольку мы имеем здесь случай одномерного течения жидкости, то справедливо следующее соотношение:
hA = h, (4)
где hA – высота области действия силы адгезии.
С учетом сказанного, при погружении трубки в жидкость, когда расстояние от верхнего торца вертикально подвешенной трубки до мениска столба жидкости в капилляре превышает величину номинальной высоты столба жидкости L ≥ hN, номинальная высота области действия силы адгезии hAN = hN. При этом величина силы адгезии не меняется σA = σAN, где σAN – номинальная величина силы адгезии, когда концевые эффекты отсутствуют.
Влияние концевых эффектов капиллярной трубки начинает сказываться тогда, когда L < hN, т.е. когда расстояние от торца трубки до мениска столба жидкости становится меньше номинальной высоты столба жидкости в капилляре.
При небольших значениях давления насыщенного пара (в случае воды) вместо уравнения (3) целесообразно принять следующее уравнение [4]:
(2σA – σLV) 2πr = hΔρgπr2 . (5)
Отсюда получается уравнение для определения величины силы адгезии
σA = (hΔρgr)/4 + σLV/2 . (6)
В рассматриваемом случае капиллярного поднятия жидкости величина силы адгезии σA (как и высота столба жидкости h) зависит от одной координаты, т.е. σA = f(x), где начало координат выберем на линии смачивания (линии трехфазного контакта). Таким образом, представляется возможным оценить зависимость σA = f(x) = f(L) (где L – расстояние от начала координат до торца трубки) c помощью экспериментально определяемой зависимости h=f(L). Последняя получается под воздействием концевых эффектов при погружении капиллярной трубки в жидкость.
Для получения большей универсальности зависимости силы адгезии введены также относительные величины: hotn = h/ hN, σAotn = σA/ σAN и Lotn = L/ hN.
2. Основные результаты и их обсуждение
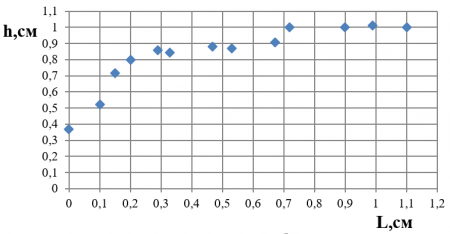
Поскольку при погружении в воду исследуемых трубок получились похожие экспериментальные зависимости влияния концевых эффектов на высоту столба жидкости в капилляре h=f(L), на рис. 2 приведена такая зависимость для трубки № 3. С помощью этой зависимости по уравнению (6) была определена соответствующая зависимость для силы адгезии (рис. 3).
Для оценки концевых эффектов на характеристики капиллярности выбрана трубка № 3 по следующей причине. Для этой трубки, как и для трубки № 4, номинальная высота столба жидкости в капилляре составляла hN=1см. Поэтому масштаб по горизонтальной оси и в размерном виде (L,см), и в относительном виде (Lotn) получается одним и тем же.
Из анализа результатов, представленных на рис. 2 и 3, следует отметить крайне неравномерный характер изменения высоты столба жидкости и суммарной силы адгезии по длине области ее действия. Напомним, что на рис. начало координат размещено на линии смачивания столба жидкости капиллярной трубки. Необходимо также отметить следующий факт.
Рис 2. Зависимость высоты столба жидкости от расстояния между торцом трубки и мениском (трубка №3).
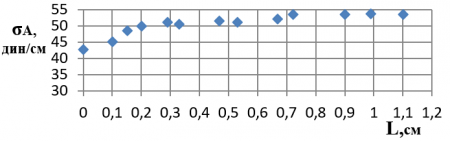Рис. 3. Зависимость величины силы адгезии от расстояния между торцом трубки и мениском столба жидкости в капилляре (трубка №3)При малых значениях Lotn<0,1 при погружении трубки, когда относительная высота столба жидкости достигала значений hotn≈0,4-0,5, мениск жидкости «толчком» прилипал к плоскости среза торца трубки. При этом визуально было видно, что расстояние от торца трубки до мениска становилось очень малым: L → 0. Следует особо отметить, что, после прилипания мениска жидкости и при дальнейшем погружении трубки, торец трубки всегда оставался сухим, т. е. столб жидкости в капилляре не поднимался выше среза торца и не растекался по торцу трубки.
Далее необходимо коснуться физики возникновения суммарной силы адгезии σAΣ, как мы ее понимаем. Из уже опубликованных работ [3,4] следует, что суммарная сила адгезии, которая действует по всей длине линии смачивания, получается в результате интегрирования по площади поверхности подложки всех элементарных сил адгезии, действующих на элементарные площадки внутри области действия силы адгезии, т.е.
σAΣ = ∫(dσA/dF)dF , (7)
где FA – суммарная площадь поверхности, где действуют силы адгезии;
σA = f(F) – распределение силы адгезии по площади ее действия.
В (7) величина dσA/dF представляет по существу силу адгезии на единицу площади, т. е. давление сил адгезии в произвольной точке указанной области.
В случае, когда имеется распределение величины силы адгезии в расчете на единицу длины линии смачивания (наш случай) справедливо следующее выражение:
σA = ∫(dσA/dL)dL , (7')
где L – высота поверхности капилляра, где действуют силы адгезии.
И здесь величина dσA/dL представляет давление сил адгезии в произвольной точке высоты L. Как известно, давление в некоторой точке равно пределу среднего давления на интервале, включающим эту точку, при стремлении интервала к нулю:
dσA/dL = lim (ΔσA/ΔL) при ΔL → 0.
Из анализа полученных на трубках зависимостей σA = f(L) по интенсивности изменения силы адгезии можно выделить три области: от очень слабого характера изменения (область I на периферии суммарной области) до сильного (область III, непосредственно примыкающая к мениску столба жидкости). В табл. 2 приведены результаты оценки изменения количественных силовых характеристик для конкретной трубки № 3.
Таблица 2.
Изменения силовых характеристик для трубки № 3
| Области действия сил адгезии | I | II | III |
Протяженность области ΔL, см | 0,7 – 1 | 0,2 – 0,7 | 0 – 0,2 |
Характер изменения силы адгезии | Очень слабый | Слабый | Сильный |
Пределы изменения силы адгезии ΔσA, дин/см | 53,5 – 53,5 | 50 – 53,5 | 42,6 – 50 |
Среднее значение давления сил адгезии ΔPA= ΔσA/ ΔL, дин/см2 | ~ 0 | 7 | 37 |
В табл. 2 представлены также средние значения давлений сил адгезии для каждой области.
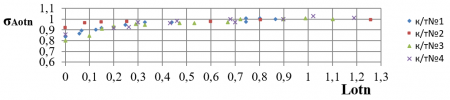
Рис. 4. Влияние концевых эффектов капиллярных трубок на относительную величину силы адгезии
На рис. 4 для исследованных трубок представлены зависимости сил адгезии в относительном виде. Из рассмотрения полученных зависимостей можно сделать следующее основное заключение: 80 – 90% суммарной силы адгезии формируется в непосредственной близости от линии смачивания.
Выводы
1. Разработана методика оценки распределения силы адгезии по высоте области ее действия в капилляре, основанная на использовании нового универсального уравнения капиллярного давления и влиянии концевых эффектов трубок на высоту капиллярного поднятия.
2. Впервые получено распределение силы адгезии по высоте области ее действия в капилляре. Показано, что 80 – 90% суммарной силы адгезии формируется в непосредственной близости от линии смачивания.
3. Для более детального изучения распределения сил адгезии вблизи линии смачивания целесообразно использовать, например, методы атомно-силовой микроскопии.
Литература
- Адамсон А. Физическая химия поверхностей. - М.: Мир, 1979. - 568 с.
- Верхоломов В. К. Новая концепция оценки системы твердое тело / жидкость / пар при смачивании. // Science and world. – 2017. № 10, V. 1, с. 11 - 15.
- Верхоломов В.К. Оценка размеров области действия сил адгезии при растекании капли жидкости по твердой поверхности. // Science and world. – 2017. № 11, V. 1, с. 11-14.
- Верхоломов В. К. Новая теория поднятия жидкости в капиллярной трубке (капиллярного поднятия). // Science and world. – 2017. № 12, V. 1, с. 22 - 24.
- Verkholomov V. K. About the New Equation of Contact Angle. // Materials of the XI international research and practice conference "Science, Technology and Higher Education". - October 19-20, 2016. - Westwood, Canada. P. 138-143.
- Verkholomov, V. K. Physical Features of the New Equation (Equation Jung - Verkholomov) of Contact Angle. // Materials of the XII international research and practice conference "Science, Technology and Higher Education". – December 21-22, 2016. – Westwood, Canada. P. 97-110.
- Young T. Essay on the Cohesion of Fluids. // M. D. For. Sec. R. S. – 1804. – P. 65-87.