Estimation of area of adhesive forces action at liquid drop spreading on the solid surface (EN) / Оценка размеров области действия сил адгезии при растекании капли жидкости по твердой поверхности (RU)
В. К. Верхоломов
Аннотация
Показано, что при растекании капли жидкости по твердой гладкой однородной поверхности вокруг капли на поверхности возникает локальная кольцеобразная область действия сил адгезии. Получено, что ширина этой области b = 0,414rK, где rK – радиус основания сидящей на поверхности капли.
// Science and World. 2017, № 11, V. 1, p. 11-13
Введение
В работах [2-5] показано, что изолированную систему твердое тело / жидкость / пар следует рассматривать, как разновидность механической системы. В рамках этой новой концепции рассмотрены силовые характеристики на линии смачивания при растекании капли жидкости по твердой гладкой однородной поверхности. Показано, что при этом вокруг сидящей капли на поверхности возникает локальная область действия сил адгезии. Величина результирующей силы адгезии, действующая по нормали к линии смачивания, зависит от поверхностных энергетических характеристик, как твердого тела, так и жидкости. Получено новое уравнение Юнга-Верхоломова равновесного краевого угла смачивания следующего вида [5]:
CosθO = (σA – σLS)/ σLV, (1)
где σA – сила адгезии на границе раздела фаз твердое тело/пар; σLS, σLV – поверхностные натяжения на границах раздела жидкость/твердое тело и жидкость/пар соответственно.
Главное отличие нового уравнения от известного уравнения Юнга состоит в том, что вместо свободной поверхностной энергии твердого тела σSV входит величина силы адгезии σA, являющейся движущей силой процесса растекания капли по твердой поверхности.
Другое отличие состоит в том, что вместо величины поверхностной энергии на границе твердое тело/жидкость σSL входит величина поверхностного натяжения на границе жидкость/твердое тело. Здесь просматривается аналогия между состоянием поверхностной молекулы жидкости на границе жидкость/пар и состоянием поверхностной молекулы жидкости на границе жидкость/твердое тело.
В первом случае на поверхностную молекулу на границе жидкость/пар, с одной стороны, действуют силы притяжения (силы когезии) со стороны ближайших молекул, находящихся в жидкости в пределах сферы ее молекулярного действия. Равнодействующая этих сил F1 направлена вглубь жидкости перпендикулярно к поверхности. С другой стороны, на эту же молекулу действуют силы притяжения со стороны жидкостных молекул, находящихся над поверхностью жидкости в парообразном состоянии. Равнодействующая этих сил F2 направлена противоположно силе F1.
Во втором случае, на поверхностную молекулу жидкости на границе жидкость/твердое тело, с одной стороны, действуют силы когезии со стороны окружающих ее молекул внутри жидкости, старающихся втянуть молекулу внутрь жидкости. С другой стороны, на эту же молекулу действуют силы притяжения со стороны частиц на поверхности твердого тела (силы адгезии). Таким образом, как силы со стороны молекул пара над поверхностью жидкости в первом случае, так и силы адгезии со стороны частиц твердой поверхности во втором случае стремятся уменьшить поверхностное натяжение жидкости.
Из приведенной картины явления следует, что сила адгезии выступает дважды. С одной стороны, она действует со стороны частиц твердой поверхности перпендикулярно к линии смачивания, являясь движущей, внешней силой процесса растекания капли жидкости. С другой стороны, она продолжает действовать и после того, как жидкость натечет на твердую поверхность. Но в этом случае сила адгезии является уже внутренней силой, которая снижает поверхностное натяжение жидкости.
Целями настоящей работы является оценка размеров области действия сил адгезии при контакте капли жидкости с твердой поверхностью.
1. Взаимодействие сил при растекании капли жидкости по твердой поверхности
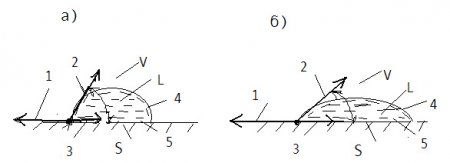
На рисунке приведена схема взаимодействия сил при растекании капли жидкости по поверхности твердого тела
Рис. Схема взаимодействия сил при растекании капли: 1- ; 2- ; 3- : 4-наружный поверхностный слой; 5-внутренний поверхностный слой
в двух состояниях капли: а) соответствует промежуточному состоянию с динамическим краевым углом θd; б) соответствует конечному состоянию равновесия с равновесным краевым углом θ0. Цифрами 1, 2, 3 на рис. обозначены σA, σLV и σLS соответственно.
Следует особо отметить, что приведенная схема взаимодействия сил при растекании капли жидкости полностью согласуется со схемой сил, представленной в работе Юнга [6]: раздел VII «Когезионное притяжение твердых тел и жидкостей».
Итак, при растекании капли жидкости перед ней на твердой поверхности локально возникает кольцеобразная зона действия сил адгезии. Физический механизм возникновения сил адгезии пока неясен. Необходимо подчеркнуть, что капля жидкости при растекании имеет два поверхностных слоя: наружный (4, см. рис.) на границе с паром и внутренний (5) на границе с твердой поверхностью. Поскольку при малых давлениях насыщенного пара силы притяжения на поверхностные жидкостные молекулы в слое (4) со стороны молекул пара существенно ниже сил притяжения на поверхностные молекулы в слое (5) со стороны частиц твердой поверхности, поверхностное натяжение в наружном слое (4) существенно больше поверхностного натяжения во внутреннем слое (5), т.е. σLV > σLS. Разумеется, речь идет об умеренных температурах системы. Образно говоря, внутренний поверхностный слой можно считать ослабленным, т.е. обладающим значительно меньшей величиной поверхностного натяжения.
Как следует из рис., на единицу длины линии растекания капли жидкости действуют три силы: сила адгезии σA (1) и силы поверхностного натяжения жидкости в наружном поверхностном слое σLV (2) и во внутреннем - σLS (3). В проекции на горизонтальную ось две силы σA и σLS являются постоянными, а проекция силы σLV – переменной величиной. Разность сил σA - σLS также является постоянной. На основании работы [1] эту разность логично назвать «адгезионным натяжением». В данном случае адгезионное натяжение является результирующей движущей силой процесса растекания капли. Проекция σLVCosθd в процессе растекания капли (в случае неполного смачивания) возрастает и в состоянии равновесия становится равной адгезионному натяжению:
(σA - σLS) = σLV Cosθ0 (2)
Таким образом, проекцию σLV Cos θd можно рассматривать в качестве «силового балансира» адгезионного натяжения:
σLV Cosθd ≤ (σA - σLS), (3)
где знак «меньше» относится к промежуточным состояниям растекающейся капли, которым соответствует динамический краевой угол θd.
2. Оценка размеров области действия сил адгезии. Обсуждение результатов
Как следует из работ [1,5], отличительной особенностью явления смачивания является тождественность поверхностных энергетических характеристик и соответствующих сил. Например, величину σLV в одно и тоже время можно рассматривать и как удельную поверхностную энергию, и как силу поверхностного натяжения, приходящуюся на единицу длины линии смачивания.
Перепишем уравнение (1) в следующем виде:
σA = σLS + σLV Cosθ0 (4)
Будем рассматривать это уравнение, как уравнение баланса удельных поверхностных энергий. Умножим обе части уравнения на одну и туже величину ωLS - величину площади круга основания сидящей капли в состоянии равновесия
σA ωLS = σLS ωLS + σLV ωLS Cosθ0. (5)
В итоге мы получили уравнение равновесия поверхностных энергий всей системы твердое тело/жидкость/пар. Из уравнения (5) следует, что в равновесном состоянии капли жидкости на твердой поверхности площадь кольцеобразной области действия сил адгезии равна площади основания капли: ωA = ωLS . (6)
Отсюда следует, что ширина кольцеобразной области действия сил адгезии:
b = 0,414rK, (7)
где rK – радиус площади круга основания сидящей капли. С учетом того, что на площади основания капли также действует сила адгезии со стороны частиц твердой поверхности, получаем радиус площади круга области действия сил адгезии:
rA = 1,414 rK . (8)
Можно, по-видимому, предположить, что соотношения (7,8) будут действовать и при растекании капли по твердой поверхности. При этом вместо уравнения (5) будет иметь место следующее неравенство:
σA ωLS' > σLS ωLS' + σLV ωLS' Cosθd, (9)
где ωLS' - текущая площадь основания капли жидкости.
Выводы
1. Показано, что перед каплей жидкости на твердой гладкой однородной поверхности возникает локальная кольцеобразная область действия сил адгезии, результирующая которых σA является движущей силой процесса растекания капли.
2. Получено, что ширина этой кольцеобразной области равна b = 0,414rK , где rK – радиус круга основания сидящей капли.
3. Целесообразно провести специальные эксперименты по оценке эпюры распределения сил адгезии по ширине кольцеобразной области с помощью, например, методов атомно-силовой микроскопии.
Литература
- Адамсон А. Физическая химия поверхностей. М.: Мир, 1979. 568 с.
- Верхоломов В.К. Новая концепция оценки системы твердое тело/жидкость/пар при смачивании // Science and world. 2017. №10. V.1. С.11-15.
- Верхоломов, В.К. О работе адгезии при смачивании твердой поверхности жидкой фазой // Science and world. 2017. №4. V.1. С. 11-14.
- Verkholomov V.K. About the New Equation of Contact Angle. // Materials of the XI international research and practice conference "Science, Technology and Higher Education". October 19-20, 2016. Westwood, Canada. P. 138-143.
- Verkholomov V.K. Physical Features of the New Equation (Equation Jung - Verkholomov) of Contact Angle. // Materials of the XII international research and practice conference "Science, Technology and Higher Education". December 21-22, 2016. Westwood, Canada. P. 97-110.
- Young T. Essay on the Cohesion of Fluids. // M. D. For. Sec. R. S. 1804. P. 65-87.
- Жалоба
- 1 168
- syshatunov от