В результате проведённого анализа показано, что при растекании капли в системе твёрдое тело/жидкость/пар со стороны частиц твёрдой поверхности одновременно действуют одинаковые по величине горизонтальные и вертикальные силы адгезии. Теплота смачивания эквивалентна работе вертикальных сил адгезии.

Одним из главных аргументов сторонников термодинамического подхода к рассматриваемой системе твёрдое тело/жидкость/пар, позволяющий считать ее термодинамической системой, связан с теплотой смачивания. Это действительный экспериментальный факт, что при иммерсионном смачивании мелкозернистых порошков твердых тел выделяется теплота. Принято, что теплотой смачивания называется теплота, которая выделяется при смачивании единицы поверхности твёрдого тела. Теплота смачивания, являющаяся основной характеристикой иммерсионного смачивания порошков твердых тел, определяется экспериментально с помощью следующего выражения [4]:

Q_см = ΔH/ω, (1)

где ΔH – теплота смачивания единицы массы твёрдого теле (мДж/г); ω – удельная поверхность твёрдого тела, т.е. поверхность единицы массы (м²/г). Теплота смачивания определяется с помощью калориметрического метода.

А так как теплота, как само понятие присуще термодинамическим системам, то логика рассуждений сторонников термодинамического подхода следующая. Теплота смачивания выделяется в процессе увеличения поверхности капли, связанного с растеканием капли жидкости по твёрдой поверхности. Это происходит в результате совершения работы сил поверхностного натяжения. В конечном счёте, это приводит к изменению (возрастанию) температуры и внутренней энергии, рассматриваемой изолированной термодинамической системы. Такое изменение в энергоизолированной системе происходит по причине гетерогенности системы твёрдое тело/жидкость/пар. И то, что справедливо для однофазной однородной изолированной системы, не подходит к рассматриваемой гетерогенной системе.

Но в таком случае полученный вывод противоречит закону сохранения энергии изолированной термодинамической системы [3]. Получается, что в такой изолированной гетерогенной системе при отсутствии энергообмена с внешней средой в результате термодинамического процесса, связанного с растеканием капли жидкости и перехода из одного равновесного состояния в другое, происходит возрастание внутренней энергии системы. Это никак не согласуется с понятием изолированной системы. Более того, это наводит на мысль, что в данном случае мы получаем частный случай вечного двигателя.

Таким образом, теплота смачивания не может служить доказательством того, что рассматриваемая система является термодинамической системой. Как было показано в работе [1], система твёрдое тело/жидкость/пар является разновидностью механической системы.

Рассмотрим теплоту смачивания в механической системе твёрдое тело/жидкость/пар.

Вначале рассмотрим следующие два примера. В первом примере на абсолютно гладкой твёрдой ровной поверхности (наподобие ледяной) лежит тяжёлый деревянный ящик, по форме представляющий прямоугольный параллелепипед. При этом коэффициент трения между основанием ящика и твёрдой поверхностью является ничтожно малым. Понятно, что достаточно небольшого усилия, чтобы передвинуть ящик на какое-либо расстояние, например, равное 5 м. Более того, ящик, обладающий определенной парусностью, может быть передвинут на тоже расстояние под действием даже небольшой силы ветра.

Во втором примере тот же ящик поместим, например, на просёлочную дорогу. В этом случае при перемещении ящика на те же 5 м потребуется приложить достаточно большое усилие и совершить работу по преодолению сил трения. Это происходит по причине большого значения коэффициента трения между ящиком и дорогой. При этом в соответствии с законом сохранения энергии механическая работа по перемещению ящика превратилась в тепло, т.е. произошла диссипация энергии. В отличие от первого примера, тяжёлый ящик на просёлочной дороге не сдвинется с места даже при ураганном ветре из-за действия больших сил трения.

Но вернёмся к нашей системе твёрдое тело/жидкость/пар. Если каплю жидкости, например, воды нанести на супергидрофобную ровную твёрдую поверхность с краевым углом смачивания, близким к 180º (θ ~ 180º), то капля примет шарообразную форму. При этом силы адгезии в уравнении краевого угла Юнга-Верхоломова (2) будут близки к нулю. Капля будет легко перекатываться по поверхности даже при ее ничтожно малом угле наклона. Капля также будет легко перекатываться под напором очень слабой струи воздуха. Получается аналогия с тяжёлым ящиком в первом примере, лежащим на гладкой ровной поверхности с ничтожно малым трением.

Но, если такую же каплю воды поместить на лиофильную гладкую твёрдую поверхность, то, во-первых, под действием сил адгезии произойдёт растекание капли по поверхности. В положении равновесия, согласно уравнению Юнга-Верхоломова, образуется некоторый краевой угол смачивания θ₀ < 90º. А, во-вторых, капля прилипнет к этой поверхности в результате действия также сил адгезии. Таким образом, получается, что при растекании капли силы адгезии действуют двояким образом. С одной стороны, они выступают в качестве движущей силы при растекании капли, а, с другой – они фиксируют каплю на поверхности, т.е. действуют аналогично силам трения во втором примере. И, чтобы сдвинуть каплю с места, потребуется наклонить поверхность с каплей на достаточно большой угол. На рис. 1 представлена схема действия сил адгезии со стороны одиночной частицы твёрдой поверхности (показана жирной точкой) вблизи линии трёхфазного контакта капли. Как видно из рисунка, результирующая сила адгезии Ϭ_A^R действует под углом 45º к твёрдой поверхности. Составляющими этой силы является сила адгезии, параллельная твёрдой поверхности, и сила адгезии, перпендикулярная к поверхности, которые равны между собой. Можно попытаться представить, что сила адгезии Ϭ_A^R является результирующей элементарных сил адгезии Ϭ_A', которые действуют на внутреннюю поверхность четверти сферы (наподобие сил давления) около одиночной частицы поверхности (рис. 2), которая на рисунке также изображена жирной точкой. На рис. 2 элементарные силы адгезии показаны только в горизонтальном и вертикальном сечениях четверти сферы. Поскольку картины действия сил адгезии в горизонтальном и вертикальном направлениях симметричны, работы сил адгезии в горизонтальном (под их действием капля растекается) и вертикальном (под их действием капля прилипает к твёрдой поверхности) направлениях равны друг другу.

Попытаемся представить, что в системе твёрдое тело/жидкость/пар действуют только горизонтальные силы адгезии, а вертикальные – отсутствуют. В этом случае горизонтальные силы адгезии равномерно размещаются по линии смачивания (периметру основания капли) и в процессе растекания капли преодолевают сопротивление ее сил поверхностного натяжения. Но при этом положение капли на твёрдой поверхности крайне неустойчиво: достаточно небольшого внешнего возмущения (например, слабого воздействия струи воздуха), чтобы капля сдвинулась с места.

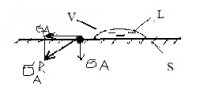
Рис. 1. Схема действия сил адгезии со стороны одиночной частицы твёрдой поверхности: S – твердая поверхность; L – жидкость; V – пар

Рис. 2. Распределение элементарных сил адгезии со стороны одиночной частицы твёрдой поверхности: А – горизонтальное сечение; В – вертикальное

Таким образом, работа вертикальных сил адгезии, связанная с прилипанием капли к твёрдой поверхности, аналогична работе сил трения в вышеприведённом примере с тяжёлым ящиком на просёлочной дороге. Поэтому эта работа не исчезает, а аналогично переходит в тепло, которое выделяется в форме теплоты смачивания в калориметре.

Следовательно, можно сделать следующий вывод: теплота смачивания эквивалентна работе сил адгезии.

В заключение попытаемся обратиться к эксперименту для подтверждения полученного вывода. К сожалению, в литературе нет достаточных систематизированных экспериментальных данных по теплоте смачивания порошков твердых тел и соответствующей величине краевых углов смачивания θ для этих порошков. В работе [4], например, приведены экспериментальные данные по теплоте смачивания некоторых твердых порошков, но без соответствующих значений θ. Поэтому, в качестве такого предварительного примера рассмотрим иммерсионное смачивание сажи в воде. Теплота смачивания для сажи составляет Q_см = 32 мДж/м² [4]. Сажа, как и графит, представляет мелкодисперсный углерод. Примем, что для этих видов углерода краевые углы смачивания одинаковы. В работе [2] для мелкодисперсного порошка графита экспериментальное значение краевого угла получено θ = 125º. Для воды поверхностное натяжение σ_LV = 72,6 мН/м [4]. Из уравнения краевого угла смачивания Юнга-Верхоломова (когда давление насыщенного пара мало) [5]

Cosθ = (2σ_A – σ_LV)/ σ_LV. (2)

Отсюда

σ_A = σ_LV(1 + Cosθ)/2. (3)

При подстановке числовых данных в уравнение (3) получим σ_A = 15,45 мДж/м². Ранее [5] было получено, что работа адгезии

W_A = 2σ_A. (4)

В итоге получаем W_A = 30,9 МДж/м².

Таким образом, в рассмотренном примере получено удовлетворительное согласование между экспериментальным значением теплоты смачивания и расчётным значением работы адгезии.

1. В результате проведённого анализа получено, что в системе твёрдое тело/жидкость/пар со стороны частиц твёрдой поверхности одновременно действуют равные по величине горизонтальные и вертикальные силы адгезии.

2. Теплота смачивания эквивалентна работе вертикальных сил адгезии.