Estimation of the values of the adhesion forces of a solid hydrophobic surface when a liquid (water) slides (EN) / Оценка величин сил адгезии твердой гидрофобной поверхности при скольжении жидкости (воды) (RU)
В. К. Верхоломов
Аннотация
Впервые получены количественные результаты о величине граничных сил адгезии при начале скольжения воды по твердой гидрофобной поверхности: σAr = 15,5 мН/м. Показано существенное, почти 6-кратное снижение сил когезии, действующих на поверхностные молекулы жидкости, при переходе от растекания капли к ламинарному течению воды.
// Science and World. 2021. № 3, p. 8–12
Введение
В работах [2, 3] уже говорилось о значительном научном и практическом значении явления скольжения жидкости вдоль гидрофобной твердой поверхности. Это явление исследовалось и теоретически, и экспериментально на протяжении последних примерно 150 лет. С целью объяснения физики явления скольжения были предложены теоретические модели: модель молекулярного скольжения [7], модель газовой прослойки между твердой поверхностью и жидкостью, а также модель кажущегося проскальзывания со снижением вязкости граничного слоя жидкости [4]. Сущность приведенных моделей сводится к тому, что между твердой поверхностью и потоком жидкости вводится некий маловязкостный псевдослой, что приводит к снижению сил трения.
Экспериментальные работы по исследованию скольжения жидкости (в основном воды) условно можно разделить на два направления. К первому относятся работы по исследованию скольжения в закрытых каналах (капиллярах, трубах). Ко второму направлению относятся работы с внешним обтеканием жидкостью (водой) гидрофобных поверхностей, например, моделей судов. Общим результатом всех экспериментальных работ была сравнительно невысокая эффективность действия от скольжения жидкости. Так, например, при турбулентном течении положительный эффект при внешнем обтекании твердых поверхностей с гидрофобным покрытием практически отсутствовал относительно гладких поверхностей без покрытия [5, 6, 8].
В отличие от других экспериментальных работ, где исследовались, в основном, интегральные характеристики скольжения жидкости (расход, средняя скорость течения, сопротивление трения) основной целью наших уже выполненных экспериментальных работ была визуальная оценка поведения пограничного слоя и потока воды в целом в условиях скольжения вдоль гидрофобной поверхности. Поскольку в закрытых каналах подобную оценку провести не представляется возможным, в качестве объекта исследования выбран открытый лоток, на внутреннюю поверхность которого наносилось супергидрофобное покрытие.
В процессе проведения экспериментов по скольжению воды в таком открытом лотке впервые в науке был получен факт отрыва потока от боковых стенок лотка, что было зафиксировано с помощью фотосъемки [2]. Следует подчеркнуть, что на всех режимах (по расходам и углам наклона лотка), которые соответствовали турбулентному режиму течения, отрыв потока происходил на всем протяжении лотка: от входа до выхода.
Целями настоящей работы были количественные оценки действующих сил адгезии твердой поверхности при скольжении жидкости.
Коротко остановимся на качественной картине течения при скольжении жидкости по твердой гидрофобной поверхности.
1. Качественная картина при скольжении жидкости по твердой гидрофобной поверхности
Следует отметить, что качественную физическую картину скольжения жидкости вдоль твердой гидрофобной поверхности невозможно объяснить с позиций термодинамического (энергетического) подхода в теории поверхностных явлений. Сущность этого явления можно раскрыть и понять только с позиций новой теории смачивания, основанной на силовом подходе, на механической концепции Юнга, т.е. с позиции взаимодействия сил, возникающих при течении жидкости по твердой поверхности.
Только механический (силовой) подход позволяет объяснить физику возникновения пограничного слоя при течении жидкости (воды) по лиофильной твердой поверхности. Как уже ранее было сказано [3], силы адгезии и когезии, определяющие процесс смачивания и растекания жидкости в статических условиях, действуют и при течении жидкости, прежде всего воды, вдоль твердой гидрофильной поверхности. В этом случае действие сил адгезии σA со стороны твердой поверхности на прилежащие молекулы жидкости превосходит действие сил когезии и внешних тангенциальных сил, стремящихся оторвать их от поверхности, т.е.
σA > (σK + στ) (1)
где σK – силы когезии, στ – внешние тангенциальные силы.
Следующий уже движущийся слой молекул начинает подтормаживаться из-за действия сил когезии между слоями т.д. Такая картина действует при ламинарном течении и в ламинарном подслое турбулентного пограничного слоя. В [3] особо подчеркнуто, что главная, превалирующая роль в образовании пограничного слоя принадлежит силам адгезии твердой поверхности.
Другая картина течения жидкости получается на твердой лиофобной поверхности с большим краевым углом смачивания θ. На такой поверхности существенно уменьшаются силы адгезии твердой поверхности, действующие на прилежащий слой жидкостных молекул. Наконец, при некотором граничном значении θ силы адгезии уменьшаются настолько, что не могут противостоять силам когезии и внешним тангенциальным силам, т.е. выполняется следующее неравенство:
(σK + στ) ≥ σA (2)
Как ранее было показано, интегральным критерием наступления явления скольжения является граничное значение краевого угла смачивания θr. Условие скольжения можно записать с помощью следующего выражения:
θ ≥ θr (3)
С учетом результатов [3] для воды можно принять θr = 125º. При скольжении жидкости (воды) происходит отрыв ранее неподвижных молекул, прилипших к поверхности, и слой этих молекул начинает перемещаться относительно стенки. В работе [3] сделан важный вывод о том, что при скольжении жидкости пограничный слой не образуется, не возникает. Одновременно в открытом лотке происходит отрыв потока воды от боковых стенок.
2. Оценка величины сил адгезии твердой поверхности при скольжении жидкости и обсуждение результатов
До настоящего момента говорилось лишь о качественной картине взаимодействия сил при наступлении явления скольжения жидкости. В соответствии с неравенством (2) скольжение наступает тогда, когда силы адгезии, действующие на поверхностные молекулы жидкости, становятся меньше суммы сил когезии и внешних тангенциальных сил. Как ранее было показано, между величинами сил адгезии и краевого угла смачивания существует однозначное соответствие. В случае, когда упругостью насыщенного пара можно пренебречь (например, для воды) уравнение Юнга-Верхоломова краевого угла имеет вид:
Cosθ0 = (2σA – σLV) / σLV (4)
Отсюда получается следующая зависимость σA от θ0:
σA = σLV (1+ Cosθ0) / 2 (5)
Следует подчеркнуть, что силы адгезии твердой поверхности сохраняются неизменными как в статических условиях растекания капли по поверхности твердого тела, так и в динамических условиях при течении жидкости. Они зависят только от краевого угла и поверхностного натяжения жидкости. На рис. 1 приведены зависимости σA = f(θ0) для нескольких жидкостей. Предположим, что граничное значение θr = 125º, полученное для воды, выполняется и для других жидкостей. При таком предположении результаты оценки соответствующих граничных сил адгезии σAr представлены в табл.
Рис. 1. Зависимости сил адгезии от краевого угла смачивания для разных жидкостей
Таблица
Величины граничных сил адгезии при θr = 125º
| Жидкость | Вода | Керосин Т-1 | Бензин Б-70 | Бензол | Формамид | Глицерол |
| σAr, мН/м | 15,5 | 5,72 | 4,82 | 6,17 | 12,42 | 13,54 |
Для оценки в первом приближении величины сил когезии при наступлении скольжения жидкости пренебрежем значением внешних тангенциальных сил в (2) и перейдем от неравенства к равенству. Тогда:
σK ≈ σAr (6)
Таким образом, при граничном значении краевого угла θ0 = θr силы когезии приближенно равны граничным силам адгезии. Так, для воды силы когезии при ее течении, согласно выражению (6), σK ≈15,5 мН/м. В тоже время в статических условиях (при растекании) силы когезии, по крайней мере, сопоставимы с поверхностным натяжением воды, т.е. величиной σLV = 72,6 мН/м. Получилось почти пятикратное уменьшение сил когезии при переходе от статических условий растекания капли воды к динамическим условиям при ее течении. Такая же картина наблюдается и для других жидкостей, представленных в таблице. Попытаемся разобраться, почему происходит такая картина при переходе от статических условий к динамическим.
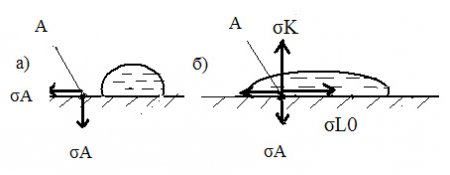
В работе [1] было показано, что при растекании капли со стороны одиночной частицы твердой поверхности вблизи линии растекания действуют две одинаковых по величине составляющих силы адгезии: горизонтальная и вертикальная (рис. 2а). Под действием горизонтальной силы адгезии происходит процесс растекания капли. Под действием вертикальной силы происходит прилипание капли к поверхности. При дальнейшем растекании капли жидкость накрывает эту одиночную частицу твердой поверхности. Естественно, что при этом горизонтальная и вертикальная составляющие силы адгезии не исчезают, а продолжают действовать уже на поверхностные молекулы жидкости. В соответствии с законом механики действие сил адгезии вызывает противодействие со стороны других молекул жидкости, окружающую поверхностную жидкостную молекулу. При этом горизонтальная составляющая этого противодействия равна поверхностному натяжению σL0, а вертикальная составляющая – силе когезии σK (рис. 2б). Нетрудно показать, что, подобно составляющим силы адгезии, поверхностное натяжение равно силе когезии: σL0 = σK, где σL0 – поверхностное натяжение, когда упругость насыщенного пара равна нулю. Таким образом, сила когезии на межфазной поверхности твердое тело/жидкость равна соответствующей величине поверхностного натяжения. При этом в случае воды, когда упругость насыщенного пара мала, имеем σK = σL0 = σLV = 72,6 мН/м. Получается, что в статических условиях растекания по лиофильной твердой поверхности силы адгезии меньше сил когезии: σA < σK. Например, для воды при θ0 = 50º σA = 59,6 мН/м.
Рис. 2. Схема сил адгезии и когезии, действующих на поверхностную молекулу жидкости при растекании капли
Как было показано выше, в динамических условиях при течении воды вдоль твердой гидрофильной поверхности силы когезии существенно уменьшаются до величины σK ≈ 15,5 мН/м, т.е. почти в 6 раз. Таким образом, при переходе от статических условий (растекание) к динамическим (течение) силы когезии, действующие на поверхностные молекулы жидкости, уменьшаются в 6 раз. Есть только одна причина для существенного уменьшения сил когезии: некоторое (ничтожно малое) увеличение расстояния между молекулами. И, если при растекании капли жидкости σA < σK, то при течении жидкости имеем уже σA > σK. По этой причине слой прилежащих к поверхности молекул жидкости прилипает к ней, а следующие слои молекул движутся относительно стенки.
Можно, по-видимому, представить следующую картину течения в ламинарном потоке и ламинарном подслое турбулентного потока.
Поскольку течение в ламинарном подслое слоистое, слои молекул не должны задевать друг друга, т.е. расстояние между слоями несколько (ничтожно мало) возрастает по сравнению с межмолекулярным расстоянием в покоящейся жидкости. В противном случае будет нарушаться слоистая структура течения. Из этого следует, что плотность движущейся жидкости будет меньше (очень незначительно) по сравнению с покоящейся жидкостью при прочих одинаковых условиях (давление, температура).
Далее. Поскольку расстояние между слоем поверхностных молекул и следующим слоем движущихся молекул возросло, силы когезии между молекулами слоев существенно уменьшились. При этом силы адгезии со стороны твердой поверхности (как при растекании, так и при течении) сохранились неизменными. Поэтому их относительное влияние значительно возросло. Благодаря этому, поверхностные молекулы жидкости оказываются жестко притянутыми к стенке, т.е. остаются неподвижными. Таким образом, действие сил адгезии на поверхностные молекулы превосходит действие как сил когезии, так и внешних тангенциальных сил, стремящихся оторвать их от поверхности. Следующий слой молекул, прилежащий к слою поверхностных молекул и начинающий движение, вследствие действия сил когезии со стороны слоя поверхностных молекул, начинает подтормаживаться. Между молекулами этого и следующего слоя также действуют силы когезии и их подтормаживающее влияние и т.д. В жидкости возникает явление вязкости и известная картина распределения скоростей по толщине ламинарного пограничного слоя.
Выводы
- Впервые получены количественные результаты о величине граничных сил адгезии при появлении скольжения воды вдоль гидрофобной твердой поверхности. Они составляют σAr = 15,5 мН/м.
- Показано существенное, почти 6-кратное снижение сил когезии, действующих на прилежащие к твердой поверхности молекулы жидкости, при переходе от статических (растекание капли) к динамическим условиям (ламинарное течение воды).
Литература
- Верхоломов, В. К. О теплоте смачивания / В. К. Верхоломов // Science and world. – 2020. – Т. 1 – № 7 – С. 8–11.
- Верхоломов, В. К. Отрыв потока от стенок при скольжении воды в открытом лотке с супергидрофобным покрытием / В. К. Верхоломов // Science and world. – 2020. – № 3 – С. 8–11.
- Верхоломов, В. К. Физические причины отрыва потока воды от стенок в лотке с супергидрофобным покрытием / В. К. Верхоломов // Science and world. – 2020. – Т. 1 – № 8 – С. 8–10.
- Виноградова, О. И. Особенности гидродинамического и равновесного взаимодействия гидрофобных поверхностей.: Дис. на соиск. уч ст. док. физ.-мат. наук / О. И. Виноградова. – М.: МГУ им. М. В. Ломоносова, 2000. – 175 с.
- Орлов, О. П. Оценка возможности применения водоотталкивающих покрытий для снижения гидродинамического сопротивления судов / О. П. Орлов, А. В. Сверчков. – СПб.: Крыл. госуд. науч. центр. – 2018. – Т. 383 – № 1 – С. 43–59.
- Пустошный, А. В. Супергидрофобные покрытия. Возможности и перспективы их применения для снижения гидродинамического сопротивления / А. В. Пустошный, А. А. Хомяков, Л. Б. Бойнович. – СПб.: Междунар. конф. по судостр. и океанотех – 2016. – С. 516–521.
- Толстой, Д. М. Молекулярная теория скольжения жидкости по твердым поверхностям / Д. М. Толстой // Докл. АН СССР. – 1952. – Т. 85 – № 5 – С. 1089–1092.
- Cose, J. W. Biomimetic super-hydrophobic coatings for friction reduction / J. W. Cose, K. Golovin, J. Barros et al // – 10th Symposium on High-Performance Marine Vehicles (HIPER'16). – Cortona, Italy, 2016. 17-19 October. – P. 477–490.
- Жалоба
- 1 044
- syshatunov от