The new theory of the liquid rise in the capillary tube (capillary rise) (EN) / Новая теория поднятия жидкости в капиллярной трубке (капиллярного поднятия) (RU)
В. К. Верхоломов
Аннотация
На основе нового уравнения Юнга-Верхоломова краевого угла смачивания разработана новая теория поднятия жидкости в капиллярной трубке (капиллярного поднятия).
// Science and World. 2017. №12, V. 1, p. 22-24
Введение
Новое уравнение Юнга-Верхоломова равновесного краевого угла смачивания было получено на основании выдвинутой концепции оценки системы твердое тело / жидкость / пар, как разновидности механической системы [7,8]. Уравнение, полностью согласующееся с механическим подходом Т. Юнга [9], имеет следующий вид:
Cosθ0 = (σA – σLS)/ σLV, (1)
где σA – сила адгезии на границе раздела фаз твердое тело/пар; σLS, σLV – поверхностные натяжения на границах раздела жидкость / твердое тело и жидкость / пар соответственно.
Главное, что отличает новое уравнение от известного классического уравнения Юнга, полученного на основании термодинамического подхода при оценке рассматриваемой системы твердое тело / жидкость / пар, состоит в том, что оно, прежде всего, является уравнением баланса сил. Вместо свободной поверхностной энергии твердого тела σSV вошла величина силы адгезии σA, которая локально возникает при контакте капли жидкости с поверхностью твердого тела.
Благодаря новому уравнению Юнга-Верхоломова краевого угла смачивания можно объяснить физическую картину растекания капли жидкости по твердой поверхности, ибо сила адгезии выступает движущей силой этого процесса.
Только с помощью нового уравнения можно, наконец, объяснить физическую сущность критического поверхностного натяжения σC, введенного Зисманом [10].
Только с помощью нового уравнения можно объяснить явление висящих капель на мокром потолке, на ветке, на выходе из негерметично закрытого крана и ответить на вопрос, почему они в течение относительно продолжительного времени не падают вниз.
Только с помощью нового уравнения можно объяснить физику капиллярных явлений, широко распространенных в природе, в окружающей нас жизни. Это, например, перемещение воды в почве; подъем воды с растворенными питательными веществами по стволу растений; смачивание (несмачивание) различного рода тканей и др. Наиболее ярким проявлением капиллярных явлений является поднятие/опускание жидкости в капиллярной трубке.
Целями настоящей работы являются, основываясь на новом уравнении Юнга-Верхоломова, рассмотреть физику явления и разработать новую теорию поднятия жидкости в капиллярной трубке (капиллярного поднятия). Вначале рассмотрим современную теорию поднятия жидкости в капиллярной трубке, основанную на термодинамическом подходе.
1. Современная теория поднятия жидкости в капиллярной трубке
Рассмотрим случай полного смачивания жидкостью внутренней поверхности капиллярной трубки. Для большей определенности возьмем стеклянную трубку, а в качестве жидкости – воду. Нальем воду в широкий сосуд (1), и опустим в него капиллярную трубку (2) (рис.1).
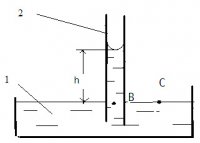
Рис. 1. Поднятие жидкости в капиллярной трубке
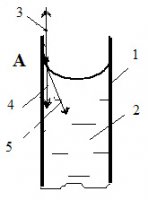
Рис. 2. Мениск столба жидкости в куапиллярной трубке: 1 - капиллярная трубка; 2 - жидкость
При полном смачивании вода в трубке поднимется на некоторую высоту h. Форму вогнутого мениска жидкости в трубке можно принять полусферической. На основании термодинамического подхода к явлению капиллярности, в современной научно-технической и учебной литературе следующим образом объясняется физика поднятия жидкости в капиллярной трубке. Над поверхностью мениска в трубке давление, равное атмосферному, больше, чем давление в жидкости (под мениском) на величину капиллярного давления Pk [1,2,5,6 и др.]
Pk = 2σLV/R = 2σLV/r , (2)
где R – радиус поверхности мениска жидкости; r – радиус капилляра; в рассматриваемом случае полного смачивания R = r.
Таким образом, получается, что в жидкости непосредственно под мениском действует вакуумметрическое давление, равное капиллярному. По этой причине жидкости в капилляре и широком сосуде не могут находится на одном уровне. В капилляре она должна подняться на такую высоту h, чтобы давление PB (в т. B) внизу капилляра и давление PC на том же уровне в т. C в широком сосуде были одинаковыми и равными атмосферному давлению P0:
PB = PC = P0 .
Тогда величину давления PBможно записать в следующем виде:
PB = P0 + Δρgh - 2σLV/r, (3)
где Δρ = ρL - ρV (разность плотностей жидкой и газовой фаз); g – ускорение свободного падения.
Отсюда, с учетом PB = P0, получается следующее выражение для высоты поднятия жидкости в капилляре:
h = 2σLV/Δρgr . (4)
По нашему убеждению, такое объяснение капиллярного поднятия жидкости не соответствует действительности. При термодинамическом подходе движущей силой капиллярного поднятия выступает поверхностное натяжение жидкости, что неверно. Ведь, как известно, основной задачей поверхностного натяжения является сокращение поверхности того или иного объема жидкости, но никак не увеличение. Первой работой, где, по-видимому, впервые была показана несостоятельность термодинамической модели применительно к капиллярным явлениям была работа [4]. Было получено, что только механическая модель оказалась правильной, хорошо согласующейся с полученными экспериментальными данными.
Рассмотрим физику и теорию капиллярного поднятия с позиций уравнения Юнга – Верхоломова краевого угла смачивания.
2. Новая теория капиллярного поднятия жидкости. Обсуждение результатов.
Для общности рассуждений рассмотрим случай неполного смачивания внутренней поверхности капиллярной трубки, т.е. θ0 > 0. В равновесном состоянии в точке трехфазного контакта т. A (рис.2) действуют три силы: сила адгезии σA (3), поверхностное натяжение на границе жидкость/твердое тело (4), поверхностное натяжение на границе жидкость/пар (5). Адгезионное натяжение, введенное в работе [1] и равное в рассматриваемом случае (σA – σLS), можно считать в качестве результирующей движущей силы процесса растекания. Следует подчеркнуть, что эта величина при капиллярном поднятии жидкости сохраняется постоянной. Адгезионное натяжение уравновешивается с помощью силового балансира σLVCosθd [3], величина которого, по мере поднятия столба жидкости, непрерывно увеличивается. В состоянии равновесия, как это следует из уравнения (1), величина адгезионного натяжения равна величине силового балансира:
(σA – σLS) = σLVCosθ0 . (5)
Вес столба жидкости в капилляре уравновешивает сила адгезионного натяжения, действующая по всей длине линии смачивания:
hΔρgπr2 = (σA – σLS)2πr . (6)
Или с использованием силового балансира из уравнения (5)
hΔρgπr2 = σLVCosθ0 2πr . (7)
Откуда величина гидростатического давления равна величине капиллярного давления в общепринятой форме:
hΔρg = Pk = 2σLVCosθ0/r . (8)
Величина капиллярного давления с использованием адгезионного натяжения из уравнения (6) получается равной
Pk = 2(σA – σLS)/ r . (9)
При небольших значениях давления насыщенного пара можно использовать также следующее выражение [3]:
Pk = 2(2σA – σLV)/ r . (9')
Здесь следует отметить два момента. Во-первых, уравнение капиллярного давления (9) наиболее полно отвечает физике явления при капиллярном поднятии жидкости, поскольку как капиллярное поднятие, так и капиллярное давление физически определяются именно величиной адгезионного натяжения – движущей силой процесса. Во-вторых, уравнение капиллярного давления (8), в котором используется величина силового балансира, имеет ограниченную область применения: его можно применять при значениях краевого угла 1800 ≥θ0 ≥ 00. В отличие от уравнения (8), уравнение (9) является универсальным: его можно использовать в указанной области изменения углов θ0 и при всех значениях коэффициента растекания.
Таким образом, гидростатическое давление в капилляре равно капиллярному давлению. В общем случае высота столба жидкости при капиллярном поднятии
h = 2(σA – σLS)/ rΔρg. (10)
Таким образом, в отличие от ныне существующей теории капиллярного поднятия, положительное избыточное капиллярное давление действует внизу капилляра (т. B на рис.1), где оно равно гидростатическому давлению. Избыточное давление вверху столба жидкости (под мениском) равно нулю.
Выводы
1. Показано, что современные представления о поднятии жидкости в капиллярной трубке весьма далеки от физики явления.
2. На основе уравнения Юнга-Верхоломова краевого угла смачивания разработана новая теория капиллярного поднятия жидкости в общем случае смачивания, где в качестве движущей силы процесса выступает адгезионное натяжение.
3. Получено новое универсальное уравнение капиллярного давления, основанное на использовании адгезионного натяжения, которое можно применять при всех значениях коэффициента растекания (S ≥ 0 и S < 0).
Литература
- Адамсон А. Физическая химия поверхностей. – М.: Мир, 1979. 568 с.
- Буховцев Б.Б., Климонтович Ю.Л., Мякишев Г.Я. Физика. – М.: Просвещение, 1973. 271 с.
- Верхоломов В.К. Оценка размеров области действия сил адгезии при растекании капли жидкости по твердой поверхности. // Science and world. – 2017. № 11, V.1, с. 11-14.
- Кашин В.В., Танутров И.Н., Свиридова М.Н. О форме поверхности мениска при капиллярном поднятии жидкости. // Расплавы. – 2011, № 5, с. 92-96.
- Фридрихсберг Д.А. Курс коллоидной химии.– Л.: Химия, 1995. 385 с.
- Эйдельман Е.Д. Физика с элементами биофизики.– М.: ГЕОТАР, 2013. 512 с.
- Verkholomov V.K. About the New Equation of Contact Angle. // Materials of the XI international research and practice conference "Science, Technology and Higher Education". - October 19-20, 2016. Westwood, Canada. P. 138-143.
- Verkholomov, V.K. Physical Features of the New Equation (Equation Jung - Verkholomov) of Contact Angle. // Materials of the XII international research and practice conference "Science, Technology and Higher Education". – December 21-22, 2016. Westwood, Canada. P. 97-110.
- Young T. Essay on the Cohesion of Fluids //M. D. For. Sec. R. S. – 1804. P. 65-87.
- Zisman W.A. Relation on the Equilibrium Contact Angle to Liquid and Solid Constitution. // Advances in Chemistry Series. American Chemical Society, Washington. - 1964. № 43, p. 1-51.
- Жалоба
- 1 340
- syshatunov от