Estimation of hydraulic losses during water flow in a tray with a superhydrophobic coating (EN) / Оценка гидравлических потерь при течении воды в лотке с супергидрофобным покрытием (RU)
В. К. Верхоломов
Аннотация
Экспериментально получено, что при турбулентном режиме течения воды в открытом лотке с текстурированным гидрофобным покрытием зависимость коэффициента гидравлического сопротивления от числа Рейнольдса соответствует квадратичному закону сопротивления, обусловленному влиянием исключительно только одной шероховатости поверхности.
// Science and World. 2022. № 5, p. 8-12
Введение
Значительный научный и практический интерес представляет эффект скольжения жидкости по гидрофобной твердой поверхности. Эффект скольжения жидкости проявляется в том, что нарушается обычная структура течения жидкости на твердой поверхности: жидкость не прилипает, а начинает скользить вдоль твердой поверхности.
Явление скольжения жидкости по гидрофобной поверхности исследовалось как в экспериментальном плане, так и в теоретическом. Кратко итоги экспериментальных исследований сводятся к следующему. Положительный эффект от скольжения жидкости (главным образом, воды) на всех существующих высокогидрофобных текстурированных покрытиях по снижению коэффициента гидравлического сопротивления зафиксирован лишь при ламинарном режиме течения: максимальное снижение составило 40-60 % относительно гладкой тестовой поверхности без покрытия. В случае турбулентного режима течения какого-либо снижения гидравлических потерь получить не удалось.
Впервые в науке проведенные экспериментальные исследования течения воды в открытом лотке с супергидрофобным покрытием [1, 2] убедительно, с помощью фотосъемки показали, что на гидрофобной поверхности со скольжением жидкости пограничный слой не образуется, не возникает, следствием чего является отрыв от стенок поверхностного слоя молекул воды и потока воды в целом. Таким образом, показано, что в этих условиях гипотеза Прандтля о прилипании жидкости к твердой поверхности не работает. Явление скольжения жидкости можно объяснить только с позиций механической концепции Юнга о силах притяжения, действующих между частицами твердой поверхности и молекулами жидкости (силы адгезии), с одной стороны, и конкурирующими силами притяжения между молекулами в самой жидкости, – с другой.
Кстати говоря, некоторые авторы в своих рассуждениях о причинах прилипания жидкости к поверхности, по-прежнему, ссылаются на ошибочную, в наше время, теорию вязкой жидкости, изложенную в классической работе [4]. Согласно этой теории, явление прилипания никак не связано со свойством смачивания тел жидкостью и гидрофобными свойствами поверхности [4, с. 372]. Этот тезис не соответствует современным представлениям теории поверхностных явлений. Полученные в последние 30-40 лет многочисленные экспериментальные результаты неопровержимо свидетельствуют о тесной связи явлений прилипания/скольжения жидкости с физикой поверхностных явлений (процессами смачивания/несмачивания). Так, например, в [3] подчеркивается, что только при высокой степени гидрофобизации (т.е. высоких краевых углах смачивания θ>90º) поверхности капилляра было обнаружено существенное увеличение расхода воды (~ в 1,5 раза), обусловленное скольжением, по сравнению с расходом тетрахлорида углерода (CCl4). А CCl4 с той же вязкостью, что и у воды, являлся уже смачивающей жидкостью этой поверхности капилляра (θ<90º) [3, с. 45]. В этой же работе сделан важный вывод о том, что явление скольжения не ограничивается разделом вода/гидрофобная поверхность и должно быть обобщено на все системы с несмачивающей жидкостью, например, на скольжение ртути по стеклянной поверхности [3, с. 27].
Таким образом, в соответствии с механической концепцией Юнга было показано [2], что основной причиной скольжения жидкости по высокогидрофобной поверхности (покрытию) является резкое уменьшение сил адгезии со стороны гидрофобной поверхности. Силы адгезии уменьшаются настолько, что уже не могут сопротивляться внешним тангенциальным силам и силам когезии со стороны соседнего движущегося слоя жидкости. Происходит отрыв ранее неподвижных молекул, прилипших к твердой поверхности. Этот слой вдруг приходит в движение и начинает перемещаться относительно стенки: начинается скольжение жидкости.
Целью настоящей работы является экспериментальное определение коэффициента гидравлического сопротивления при скольжении воды в лотке с супергидрофобным покрытием.
1. Методика определения гидравлических потерь
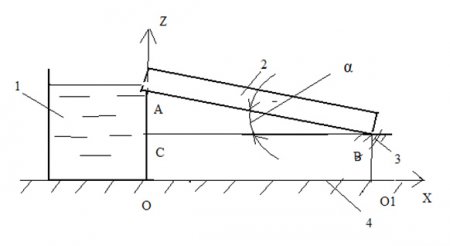
Рис. 1. Расчетная схема экспериментальной установки: 1 – бак с водой; 2 – открытый лоток; 3 – задняя опора; 4 – поверхность отсчета
Поскольку течение воды в открытом лотке с высокогидрофобным покрытием происходило с отрывом потока от стенок лотка, т.е. без образования пограничного слоя, потери на трение отсутствовали. В этом случае потери от гидравлического сопротивления сводятся только к потерям от шероховатости текстурированного покрытия. Принятый порядок расчетов коэффициента сопротивления от шероховатости состоит из двух этапов. На первом этапе определяются экспериментальные значения коэффициентов скорости течения и относительные потери скорости, на втором – коэффициенты сопротивления от шероховатости.
На рис. 1 представлена расчетная схема установки, подробное описание которой приведено в [1]. В бак (1) и открытый лоток (2) непрерывно поступал определенный расход воды. Оценку гидравлических потерь проведем при номинальном расходе 50 мл/с.
1.1. Определение коэффициентов скорости течения воды
Приняты следующие условные обозначения.
WД.П – эксперимент. значение скорости течения в лотке с покрытием;
WД – эксперимент. значение скорости течения в лотке без покрытия;
Wа.П, Wа – значения идеальной скорости в лотке с покрытием и без;
φП = WД.П / Wа.П – коэффициент скорости в лотке с покрытием;
φ = WД / Wа – коэффициент скорости в лотке без покрытия;
Δ φШ = 1 – φП – относит. потери скорости, вызванные шероховатостью;
ΔφΣ = 1 – φ – относит. потери скорости, вызванные шероховатостью и наличием пограничного слоя;
Δ φП.С. ~ ΔφΣ – φШ – относит. потери скорости, вызванные наличием пограничного слоя;
1.1.1. Значение идеальной скорости в лотке с покрытием
Wа.П = Wвх.П + Wi, (1)
где Wi – скорость течения, вызванная перепадом высот на концах лотка;
Wвх.П – скорость на входе в лоток с покрытием, которая определяется по экспериментальным данным при горизонтальном положении лотка.
1.1.2. Значение идеальной скорости в лотке без покрытия
Wа = Wвх + Wi, (2)
Wвх – скорость на входе в лоток без покрытия, которая определяется по экспериментальным данным при горизонтальном положении лотка.
1.1.3. Скорость течения, вызванная перепадом высот на концах лотка
Величину этой скорости определим из уравнения Бернулли (см. рис. 1.)
ρgz0 + P0 = ρgz1 + P0 + (ρWi2) /2, (3)
где z0 – геодезическая высота входного сечения лотка (АО на рис. 1);
z1 – геодезическая высота выходного сечения лотка (ВО1 на рис. 1);
Р0 – атмосферное давление; ρ – плотность воды.
Из уравнения (3) получаем величину скорости, вызванную перепадом высот:
Wi = √2gh, (4)
где h = z0 – z1 = АС, АС = АВ·Sinαι, АВ = 63 см.
В результате оценки получены следующие значения скорости на входе в лоток: Wвх.П = 20,6 см/с; Wвх = 11,9 см/с. Эти значения сохранялись постоянными при всех углах наклона лотка.
Окончательные результаты определения значений коэффициентов скорости и относительных потерь скорости представлены в табл. 1,2.
Таблица 1.
Значения коэффициентов скорости течения воды
| α0 | WД.П, см/с | Wа.П, см/с | WД, см/с | Wа, см/с | φП | φ |
| 0 | 24,6 | 31,5 | 15 | 22,8 | 0,78 | 0,66 |
| 0,5 | 35,7 | 45 | 19,2 | 36,3 | 0,79 | 0,53 |
| 1 | 43,9 | 55,1 | 23,9 | 46,4 | 0,8 | 0,51 |
| 1,75 | 52,4 | 66,3 | 26,3 | 57,6 | 0,79 | 0,46 |
Таблица 2.
Относительные потери скорости течения воды
| α0 | Δ φШ | ΔφΣ | Δ φП.С |
| 0 | 0,22 | 0,34 | 0,12 |
| 0,5 | 0,21 | 0,47 | 0,26 |
| 1 | 0,2 | 0,49 | 0,29 |
| 1,75 | 0,21 | 0,54 | 0,33 |
1.2. Коэффициенты сопротивления от шероховатости покрытия
1.2.1. Суммарные потери от сил гидравлического сопротивления
Потери от сил гидравлического сопротивления в лотке с покрытием определим из следующего уравнения:
ζ · (ρWд.п2)/2 = (ρWа.п2)/2 – (ρWд.п2)/2, (5)
где ζ – суммарный коэффициент сопротивления от шероховатости;
1.2.2. Разделив обе части уравнения (5) на (ρWд.п2)/2, получим
ζ = 1/ φп2 – 1. (6)
Здесь ζ представляет суммарный коэффициент гидравлических потерь, отнесенный ко всей относительной длине лотка (L/D).
1.2.3. Число Рейнольдса по гидравлическому диаметру
ReDг = (Wд.п DГ) /ν+15, (7)
где DГ – гидравлический диаметр; ν+15 = 0,0115 см2/с – кинемат. вязкость.
В табл. 3 представлены результаты определения суммарных коэффициентов гидравлических потерь для принятого супергидрофобного текстурированного покрытия.
Таблица 3.
Значения суммарного коэффициента гидравлических потерь
| α0 | WД.П, см/с | DГ, см | ReDг | ζ |
| 0 | 24,6 | 4,5 | 9470 | 0,64 |
| 0,5 | 35,7 | 3,9 | 12100 | 0,6 |
| 1 | 43,9 | 3,8 | 14500 | 0,56 |
| 1,75 | 52,4 | 4,7 | 21320 | 0,6 |
2. Обсуждение полученных результатов
Как следует из табл. 3, для принятого номинального расхода воды Q = 50 мл/c и при всех углах наклона лотка (0-1,75º) течение в открытом лотке соответствовало турбулентному режиму (Re>Reкр).
Из сопоставления коэффициентов скорости, полученных на лотке с покрытием и без (табл. 1), можно сделать два заключения. Во-первых, уровень значений коэффициентов скорости в лотке с покрытием был значительно выше, чем в лотке без покрытия. Во-вторых, виден разный характер изменения зависимостей от скорости течения WД. В то время, как в лотке без покрытия коэффициент скорости существенно уменьшался при возрастании WД (примерно в 1,4 раза), в лотке с покрытием он сохранялся примерно постоянным на уровне 0,79.
Аналогичный характер изменения имели зависимости для относительных потерь скорости.
Причина такого изменения соответствующих зависимостей заключается в следующем. На лотке без покрытия относительные потери скорости безотрывного течения воды обусловлены гидравлическим сопротивлением от двух видов потерь: физических потерь, связанных с межмолекулярным взаимодействием и образованием пограничного слоя, и инерционных (механических) потерь, связанных с шероховатостью поверхности. На лотке с супергидрофобным текстурированным покрытием, вследствие отрыва потока от стенок и отсутствия пограничного слоя, остались только относительные потери скорости, связанные с потерями от шероховатости.
В табл. 2 приведены также относительные потери скорости, связанные с наличием одного только пограничного слоя в лотке без покрытия. Здесь необходимо дать следующее пояснение. Эти потери определены при допущении о том, что шероховатости поверхностей лотка с покрытие и без одинаковы. Поскольку мы не располагаем данными по величине шероховатостей, эта величина ΔφП.С носит в основном качественный характер.
В табл. 3 представлены результаты экспериментального определения суммарного коэффициента гидравлических потерь в лотке с покрытие, связанных с шероховатостью самого текстурированного покрытия.
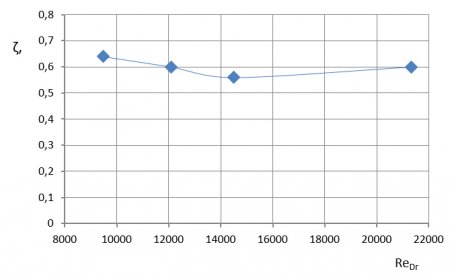
Как следует из рис. 2, экспериментальные точки расположились параллельно оси чисел Рейнольдса. Это соответствует квадратичному закону сопротивления, который, как известно, обусловлен исключительно влиянием одной лишь шероховатости. Именно шероховатость текстурированных гидрофобных покрытий полностью нивелирует большой ожидаемый эффект от скольжения жидкости.
Рис. 2. Изменение коэффициента гидравлического сопротивления по числу Re при течении воды в лотке с супергидрофобным покрытием
Выводы
1. Экспериментально получено, что при турбулентном режиме течения в лотке с высокогидрофобным текстурированным покрытием зависимость коэффициента гидравлического сопротивления от числа Рейнольдса соответствует квадратичному закону сопротивления, обусловленному влиянием одной лишь шероховатости.
2. Показано, что большой положительный эффект от скольжения жидкости (воды) при турбулентном течении полностью нивелируется сопротивлением от шероховатости текстурированных покрытий.
Литература
- Верхоломов, В. К. Отрыв потока от стенок при скольжении воды в открытом лотке с супергидрофобным покрытием / В. К. Верхоломов // Science and world. – 2020. – № 3. – Т. 1. – С. 8-11.
- Верхоломов, В. К. Физические причины отрыва потока воды от стенок в лотке с супергидрофобным покрытием / В. К. Верхоломов // Science and world. – 2020. – № 8. – Т. 1. – С. 8-10.
- Виноградова, О. И. Особенности гидродинамического и равновесного взаимодействия гидрофобных поверхностей: Дисс. на соиск. уч ст. д.ф.-м. н. / О. И. Виноградова. – М.: МГУ им. М. В. Ломоносова, 2000. – 175 с.
- Лойцянский, Л. Г. Механика жидкости и газа. – 7-е изд., испр. / Л. Г. Лойцянский. – М.: «Дрофа», 2003. – С. 840.
- Жалоба
- 528
- syshatunov от