Hanging liquid drop (EN) / Висящая капля жидкости (RU)
В. К. Верхоломов
Аннотация
С позиции механической концепции Юнга предложена физическая модель образования и развития висящей капли. Разработана методика расчета динамики роста висящей капли на первом этапе с преобладающим воздействием сил адгезии. Показано, что размеры висящей капли существенно зависят от шероховатости твердой поверхности.
// Science and World. 2022. № 9, p. 12-15
Введение
Определенный научный и практический интерес представляют физические процессы, протекающие при образовании висящих (висячих) капель жидкости. В качестве жидкости, в подавляющем числе случаев, фигурирует вода.
Висящие капли достаточно широко используются в науке и технике. Так, например, метод с использованием висящей капли применяется в микробиологии для изучения под микроскопом размножения и развития различного рода микроорганизмов в живом состоянии [5]. Метод висящей капли (сталагмометрический метод) применяется также для измерения величины поверхностного натяжения исследуемой жидкости [4].
С висящими каплями мы часто сталкиваемся в бытовых условиях. Висящие капли образуются, например, на поверхности потолка в помещении с большим испарением воды, на выходе из патрубка неплотно закрытого крана, на горизонтальных ветвях кустарников в дождливую погоду и т. д.
Однако до сих пор процессы образования висящих капель объясняются с термодинамической позиции, т.е. когда система твердое тело/жидкость/пар рассматривается, как термодинамическая система. При этом используется известное уравнение Юнга для краевого угла смачивания, основанное на соотношении поверхностных энергий на границах раздела фаз. Так, в работе [3] с помощью вариационного метода получены решения задач о профилях висящих и сидящих капель для случаев малых чисел Бонда B1~0,1 т.е. малых объемов капель, где B1 = gρVk2/3/ϬLV, g – ускорение свободного падения, ρ-плотность жидкости, Vk – объем капли, ϬLV – поверхностное натяжение на границе жидкость/пар. При этом значительная роль в образовании висящих капель приписывается величине поверхностного натяжения жидкости. Такой подход нельзя считать правомерным, так как известно, что поверхностное натяжение направлено на уменьшение поверхности капли, но никак не на увеличение поверхности растущей висящей капли.
Целями настоящей работы являются: оценка физической картины динамики роста висящей капли и разработка методики расчета развития висящей капли жидкости (на примере воды) на начальном этапе. Будет рассмотрен часто встречающийся на практике случай роста капли в помещении с интенсивным испарением воды.
1. Физическая картина образования висящей капли жидкости
В отличие от имеющихся работ, физическую картину образования и развития висящей капли жидкости рассмотрим с позиции механической концепции Юнга к системе твердое тело/жидкость/пар. Только эта концепция, рассматривающая систему твердое тело/жидкость/пар, как разновидность механической системы, позволяет ответить на основной вопрос. Почему капля воды на мокром потолке может висеть достаточно продолжительное время, а не падает вниз, как того требует поверхностное натяжение жидкости?
В работе [1] достаточно подробно была рассмотрена физическая картина растекания сидящей на горизонтальной гладкой поверхности капли жидкости. Было показано, что при этом со стороны одиночной частицы твердой поверхности вблизи линии растекания действуют две одинаковых по величине составляющих элементарной силы адгезии: горизонтальная и вертикальная. Под действием горизонтальной силы происходит процесс растекания капли. Под действием вертикальной силы происходит ее прилипание к поверхности.
Подобная картина будет происходить и в случае висящей на потолке капли. Но в отличие от сидящей на поверхности капли, сохраняющей неизменным объем, динамика развития висящей капли будет другая. На потолке с интенсивным испарением воды в помещении будет происходить процесс непрерывной конденсации пара на потолке, что вызывает непрерывное возрастание массы висящих капель с последующим падением. Из наблюдений за развитием висящих капель можно сделать два заключения.
Во-первых, величина радиуса основания капли, висящей на потолке, в процессе возрастания ее массы сохраняется неизменной.
Во-вторых, поверхность растущей висящей капли близка к сферической. То, что форма капли близка к сферической, подтверждают также результаты расчетов работы [3].
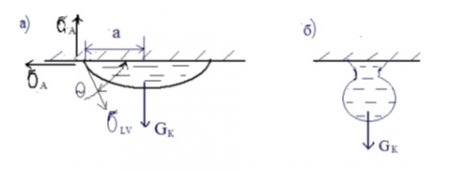
Рис. 1. Схема висящей капли на мокром потолке:
а) на первом этапе; б) на втором этапе перед падением капли
В первом приближении динамику роста с последующим падением висящей капли можно разбить на два этапа. На первом (начальном) этапе преобладает влияние сил адгезии, на втором – сил поверхностного натяжения.
На рис. 1а представлена схема положения висящей капли на первом этапе, на рис. 1б – схема капли на втором этапе перед падением. Как следует из рис. 1а, на висящую каплю действуют три силы: сила адгезии (горизонтальная и вертикальная составляющие ϬА), сила поверхностного натяжения воды ϬLV и сила веса капли Gк. То, что в процессе увеличения массы капли динамический краевой угол непрерывно возрастает, можно рассматривать, как процесс непрерывного уменьшения кажущейся силы адгезии.
Таким образом, формулу уравнения Юнга-Верхоломова можно представить в следующем виде в случае, когда мала упругость насыщенного пара:
Cosθд = (ϬА' – ϬLV)/ ϬLV, (1)
где величина ϬА' имеет следующий вид:
ϬА' = 2 ϬА – Gк'/πdк, (2)
где ϬА – номинальная величина силы адгезии, когда Gк'~0; Gк' – текущий вес висящей капли.
Первый этап заканчивается, когда числитель ур. (1) становится равным нулю. При этом создаются условия для отрыва капли.
На втором этапе рост массы капли с последующим отрывом и падением связаны с действием сил поверхностного натяжения. Эти силы отождествляют с некоей эластичной сферической сумкой, удерживающей некоторое время растущую массу висящей капли. Момент отрыва и падения капли совпадает с моментом образования шейки в месте крепления капли к потолку (рис. 1б).
2. Методика расчета динамики роста висящей капли на первом этапе
При расчете динамики роста капли приняты следующие допущения.
- В качестве исследуемой жидкости принята вода.
- Поверхность потолка гидрофильная, однородная, ровная и гладкая.
- Поверхностное натяжение и плотность воды в процессе роста капли сохраняются неизменными.
- Капли в процессе роста сохраняют форму шарового сегмента.
- Радиус основания капли в процессе ее роста не изменяется.
Поскольку поверхность потолка мокрая (покрыта пленкой воды), номинальная сила адгезии имеет следующий вид: ϬА = ϬLV. Подставляя это выражение в уравнения (1, 2), окончательно получим:
Cosθд = (ϬLV – Gк'/2πa)/ ϬLV, (3)
или
Cosθд = 1 – Gк'/2πa ϬLV, (3').
Из ур. (3) следует основное условие сохранения растущей висящей капли от действия кажущейся силы адгезии:
(ϬLV – Gк'/2πa) > 0, (4).
Когда кажущаяся сила адгезии становится равной нулю, создаются условия для отрыва капли, обусловленные действием сил адгезии.
Определим величину радиуса основания капли в конце первого этапа, т.е. когда неравенство (4) превращается в равенство:
(ϬLV – Gк/2πa) = 0, (5).
При этом краевой угол θд = 900, а капля принимает форму полусферы
Gк = Vкρg = 2πa ϬLV, (6).
После соответствующих преобразований получаем выражение для определения радиуса основания капли в этом случае
a = √ 3 ϬLV/ρg, (7).
В случае воды имеем a = 0,471 см и вес капли Gк = 214,7 дин. Из ур. (3) можно определить, как изменяется величина θд по мере увеличения веса капли (табл. 1).
Таблица 1.
Изменение θд при возрастании веса висящей капли
| Gк,', дин | 10 | 30 | 50 | 100 | 150 | 200 | 214,7 |
| θд0 | 17,5 | 30,6 | 39,9 | 57,7 | 72,5 | 86,1 | 90 |
3. Обсуждение результатов
С помощью разработанной методики представляется возможным определить размер капли в конце первого этапа ее развития. В случае воды получились не очень высокие значения радиуса основания и веса капли: a = 0,471 см; Gк = 214,7 дин, т.е. диаметр основания получился менее 1 см. В бытовых условиях можно наблюдать висящие капли значительно больших размеров. В чем же причина такого несоответствия? Все дело в том, что полученный размер капли определен при основном допущении о том, что поверхность потолка гидрофильная, горизонтальная и гладкая. На самом деле поверхность любого потолка является шероховатой.
Как известно, в случае гомогенного процесса растекания капли действует правило Венцеля вида [6]:
Cosθ=KШCosθ0, (8).
где θ0 – равновесное значение краевого угла смачивания для гладкой поверхности; KШ – коэффициент шероховатости, т.е. отношение площади шероховатой поверхности основания капли к ее проекции на горизонтальную плоскость; θ – эффективное значение краевого угла смачивания.
Ранее в работе [2] была установлена строго пропорциональная зависимость между величинами Cosθ0 и ϬА: Cosθ0~ϬА. Поэтому справедливой можно считать следующую зависимость: Cosθ~KШ ϬА = KШ ϬLV, так как для мокрой гладкой поверхности ϬА= ϬLV. С учетом сказанного выражение для определения размера висящей капли на шероховатой поверхности примет следующий вид:
a=√3KШϬLV/ρg, (9).
В табл. 2 представлены результаты расчетов размера и веса капли в зависимости от коэффициента шероховатости KШ.
Таблица 2.
Влияние шероховатости на характеристики капли
| KШ | 1 | 1,5 | 2 | 2,5 | 3 | 4 | 5 | 6 |
| а, см | 0,47 | 0,57 | 0,66 | 0,74 | 0,81 | 0,94 | 1,05 | 1,15 |
| Gк,дин | 214,7 | 379,6 | 588,6 | 831,9 | 1090 | 1704 | 2376 | 3122 |
Выводы
1. Предложена двухэтапная физическая модель образования и развития висящих капель. На первом этапе преобладающая роль принадлежит силам адгезии, на втором этапе – силам поверхностного натяжения.
2. Разработана методика расчета динамики роста висящих капель на первом этапе.
3. Показано существенное влияние шероховатости поверхности потолка на размер и вес висящей капли.
Литература
- Верхоломов В. К. Оценка величин сил адгезии твердой гидрофобной поверхности при скольжении жидкости (воды) / В. К. Верхоломов // Science and world. – 2021. – Т. 1 – № 3 – С. 8-12.
- Верхоломов В. К. О новом уравнении краевого угла смачивания / В. К. Верхоломов // Materials of the XI international research and practice conference «Science, Technology and Higher Education». October 19-20, 2016. Westwood, Canada. – P. 138-143.
- Галактионов Е. В. Приближенные формулы, описывающие профили лежащих и висящих капель в случае малых чисел Бонда и сильной смачиваемости / Е. В. Галактионов, Н. Е. Галактионова, Э. А. Тропп // ЖТФ. – 2016. – Т. 86 – Выпуск 12 – С. 17-24.
- Григорьев Г. А. Методы определения поверхностного натяжения жидкостей и энергии твердой поверхности / Г. А. Григорьев, В. Я. Киселев, В. С. Копытин. – М.: МИТХТ им. М.В. Ломоносова, 2005. – 73 с.
- Руководство по микробиологической диагностике инфекционных болезней / под ред. Матвеева К. И. – М.: 1973. – 25 с.
- Сумм Б. Д. Физико-химические основы смачивания и растекания / Б. Д. Сумм, Ю. В. Горюнов. – М.: Химия, 1976. – 232 с.
- Жалоба
- 471
- syshatunov от