The critical surface tension of wetting and its connections with surface specifications on the interphase boundaries (EN) / Критическое поверхностное натяжение смачивания и его связи с поверхностными характеристиками на границах раздела фаз (RU)
В. К. Верхоломов
Аннотация
На основе нового уравнения Юнга – Верхоломова краевого угла смачивания получено уравнение критического поверхностного натяжения. Установлено, что в случае смачивания неполярных твердых тел неполярными жидкостями (случай Зисмана) критическое поверхностное натяжение равно соответствующей величине поверхностной энергии твердого тела.
// Science and World. 2019. № 2, V. 1, p. 14-17
Введение
Значительный практический интерес в теории смачивания вызывает величина, называемая критическим поверхностным натяжением смачивания [1-6]. Понятие о критическом поверхностном натяжении в теорию смачивания введено Зисманом [8]. Оно основано на экспериментальных данных, которые были получены при смачивании низкоэнергетических твердых тел различными однокомпонентными низкоэнергетическими жидкостями. При этом рассматривался случай физического смачивания (отсутствие химических реакций, растворения и др.). Было получено, что при смачивании неполярных твердых тел (например, полиэтилена, тефлона) неполярными жидкостями (гомологический ряд n-алканов) косинус краевого угла возрастает при уменьшении поверхностного натяжения жидкостей. При этом получалась зависимость Cosθ = f(σLV), близкая к линейной. Критическое поверхностное натяжение смачивания σС определялось, как абсцисса точки пересечения указанной зависимости с прямой Cosθ = 1. Таким образом, критическое поверхностное натяжение по существу является граничной точкой, характеризующей переход от ограниченного смачивания (σLV > σС) к полному (σLV ≤ σС). Было установлено также, что величина σС мало зависит от свойств смачивающих жидкостей, а зависит от поверхностных характеристик соответствующих твердых тел.
В настоящее время экспериментально найдены значения критического поверхностного натяжения σС многих твердых тел, в особенности полимеров. Химические аспекты вопроса о связи σС с поверхностными характеристиками твердых тел были исследованы во многих работах [3,8]. Показано, например, что замещение водорода на хлор в молекуле полиэтилена приводит к возрастанию σС и, соответственно, к улучшению смачиваемости хлорзамещенных полимеров. Поэтому в настоящей работе остановимся только на физической стороне вопроса, попытаемся рассмотреть и выявить его связи с поверхностными характеристиками на границах раздела фаз при смачивании. При этом под поверхностными характеристиками на границах фаз будем понимать, как энергетические, так и силовые характеристики.
1. Связи критического поверхностного натяжения с поверхностными характеристиками на границах фаз при смачивании
Из уравнения Юнга краевого угла смачивания получается следующее соотношение, связывающее критическое поверхностное натяжение с поверхностными энергетическими характеристиками на границах фаз [6]:
σС = σSV - σSL, (1)
где σSV, σSL - поверхностные энергии на границах фаз твердое тело/пар и твердое тело/жидкость соответственно.
Некоторые исследователи были склонны отождествлять σС с σSV, но сам Зисман был более осторожным и указывал, что σС пропорционально σSV, так как не был уверен, что σSL = 0.
Как нам представляется, наибольшая ясность в вопросе связи критического поверхностного натяжения с поверхностными характеристиками на границах фаз получается, если вместо термодинамического подхода к процессу смачивания и уравнения Юнга использовать механический подход и новое уравнение Юнга – Верхоломова краевого угла смачивания. При этом будут рассмотрены следующие четыре случаи:
I. Смачивание полярного твердого тела полярными жидкостями.
II. Смачивание полярного твердого тела неполярными жидкостями.
III. Смачивание неполярного твердого тела полярными жидкостями.
IV. Смачивание неполярного твердого тела неполярными жидкостями (случай Зисмана).
При этом первый случай является общим, а остальные - частными. Рассмотрим последовательно эти случаи.
1.1. Смачивание полярного твердого тела полярными жидкостями
Из нового уравнения Юнга – Верхоломова краевого угла смачивания [7]
Cosθ0 = (2σA - σLV) / σLV, (2)
получается следующее уравнение для определения величины критического поверхностного натяжения в общем виде:
σС = σLVd + σLVp = √σSVd σLVd + √σSVp σLVp = σA, (3)
где σSVd, σLVd – дисперсионные составляющие поверхностных энергий на границах твердое тело/пар и жидкость/пар соответственно;
σSVp, σLVp – полярные составляющие поверхностных энергий на границах твердое тело/пар и жидкость/пар соответственно.
Таким образом, из уравнения (3) следует важный вывод о том, что как в общем, так и в частных случаях величина критического натяжения всегда равна соответствующей силе адгезии. Можно отметить, что в отличие от величины свободной поверхностной энергии, сохраняющей постоянное значение для конкретного твердого тела (σSV = Const) возникающая при смачивании сила адгезии зависит от энергетических характеристик и твердого тела, и жидкости. Поэтому при смачивании конкретного твердого тела разными жидкостями сила адгезии будет переменной величиной (σA = var).
Рассмотрим связь критического поверхностного натяжения σС с поверхностной энергией σSV на примере конкретного твердого тела. В качестве такого фиксированного полярного тела примем пластик поливинилфторид ( σSV=36,7; σSVd=31,3; σSVp= 5,4 мДж/м2), а неполярого тела – парафин (σSV=25,4 мДж/м2) [6]. В качестве полярных жидкостей были приняты: вода (σLV=72,6; σLVd=21,8; σLVp=50,8 мДж/м2), этиленгликоль (σLV=48; σLVd=29;σLVp=19 мДж/м2), диметилсилоксан (σLV=19; σLVd=16,9; σLVp =2,1 мДж/м2). Неполярные жидкости: н-гептан (σLV=18,4 мДж/м2), циклогексан (σLV=25,5 мДж/м2), декалин (σLV=29,9 мДж/м2) [2].
Для определения величины σС в каждом случае был использован расчетный метод, который можно назвать «методом гипотетических жидкостей». Он заключается в следующем. Для каждой из вышеперечисленных жидкостей получают ряд гипотетических жидкостей. Например, гипотетические жидкости на основе воды получаются следующим образом. Зафиксируем одну из составляющих поверхностного натяжения и будем изменять другую составляющую таким образом, чтобы получить равенство по уравнению (3). Но при этом каждая гипотетическая жидкость должна оставаться полярной. Результаты расчета для ряда на основе воды приведены в табл. 1.
Таблица 1.
Жидкости на основе воды (σLVd=21,8 мДж/м2=Const)
| σLVp, мДж/м2 | 30 | 20 | 15 | 13 | 12,6 |
| σA, мН/м | 38,8 | 36,6 | 35,2 | 34,6 | 34,4 |
| σLV, мдж/м2 | 51,8 | 41,8 | 36,8 | 34,8 | 34,4 |
| Cosθ | 0,5 | 0,751 | 0,913 | 0,987 | 1 |
Как следует из табл., для ряда полярных жидкостей на основе воды критическое поверхностное натяжение составило σС=34,4 мН/м. Аналогичные результаты были получены для рядов других полярных жидкостей. На рис.1 приведены графики зависимостей Cosθ=f(σLV) для рассмотренных рядов жидкостей.
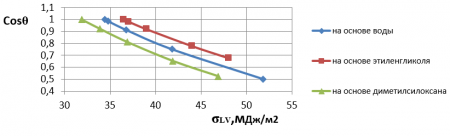
Рис. 1. Зависимости Cosθ=f(σLV) для поливинилфторида.
В табл. 2 представлены значения критических поверхностных натяжений.
Таблица 2.
Критические поверхностные натяжения для поливинилфторида
| Полярные жидкости | На основе воды | На основе этиленгликоля | На основе диметилсилоксана |
| σС, мН/м | 34,4 | 36,5 | 31,9 |
Таким образом, полученные результаты показывают, что в общем случае смачивания полярного твердого тела полярными жидкостями отсутствует однозначная зависимость между σС и σSV: для каждого полярного тела можно получить множество значений σС.
1.2. Смачивание полярного твердого тела неполярными жидкостями
В этом случае поверхностные энергии неполярных жидкостей будут: σLV= σLVd; σLVp=0.
При подстановке этих значений в уравнение (3) получим σС = σLV = √σSVd σLV (4)
Отсюда σС = σSVd. (4')
Таким образом, в этом случае критическое поверхностное натяжение равно дисперсионной составляющей твердого тела
1.3. Смачивание неполярного твердого тела полярными жидкостями
В этом случае имеем: σSV= σSVd; σSVp=0. При подстановке этих значений в общее уравнение критического поверхностного натяжения (3) получим следующее выражение:
σС = σLVd + σLVp = √σSV σLVd = σA. (5)
Отсюда можно получить соотношение для σSV
σSV = σС2 / σLVd = (σLVd + σLVp)2 / σLVd . (5')
Полученные выражения не показывают явную однозначную зависимость между σС и σSV. Попытаемся установить связь между этими величинами с помощью метода гипотетических жидкостей. Как уже было сказано, в качестве неполярного твердого тела выбран парафин (σSV=25,4 мДж/м2). Будем рассматривать три ряда гипотетических жидкостей на основе воды. этиленгликоля и диметилсилоксана, которые уже применялись в первом случае. Естественно, что сами жидкости в рядах будут другими. В табл. 3 представлены результаты расчетов для ряда жидкостей на основе воды.
Таблица 3.
Жидкости на основе воды (σLVd=21,8 мДж/м2=Const)
| σLVp, мДж/м2 | 8 | 6 | 4 | 2 | 1,7 |
| σA, мН/м | 23,5 | 23,5 | 23,5 | 23,5 | 23,5 |
| σLV, мдж/м2 | 29,8 | 27,8 | 25,8 | 23,8 | 23,5 |
| Cosθ | 0,577 | 0,691 | 0,822 | 0,975 | 1 |
Таким образом, для ряда жидкостей на основе воды критическое поверхностное натяжение составило σС=23,5мН/м. Аналогичные расчеты проведены для жидкостей на основе этиленгликоля (σС=30,1мН/м) и диметилсилоксана (σС=23мН/м). Для этого случая, как и для первого случая, отсутствует однозначная зависимость между σС и σSV.
1.4. Смачивание неполярного твердого тела неполярными жидкостями (случай Зисмана)
В этом случае имеем: σSV= σSVd; σSVp=0; σLV=σLVd; σLVp=0.
При подстановке этих значений в уравнение (3) получим следующее уравнение:
σС = σLV = √σSV σLV (6)
откуда σС = σSV. (6')
Таким образом, в случае Зисмана критическое поверхностное натяжение равно величине поверхностной энергии твердого тела.
На основании полученных результатов можно сделать следующие выводы.
Выводы
1. На основе нового уравнения Юнга – Верхоломова краевого угла смачивания для общего случая смачивания полярных твердых тел полярными жидкостями получено уравнение критического поверхностного натяжения.
2. Установлено, что в общем случае смачивания полярных твердых тел полярными жидкостями между величинами критического поверхностного натяжения и поверхностной энергии отсутствует однозначная зависимость: для конкретного твердого тела существует множество значений σС.
3. Показано, что для случая Зисмана (смачивание неполярных твердых тел неполярными жидкостями) критическое поверхностное натяжение равно соответствующей величине поверхностной энергии твердого тела.
Литература
- Адамсон, А. Физическая химия поверхностей. – М.: Мир, 1979. – 568 с.
- Григорьев Г.А., Киселев В.А., Копытин В.С. Методы определения поверхностного натяжения жидкостей и поверхностной энергии твердых тел. – М.: МИТXТ им. М.В. Ломоносова, 2005. 70с.
- Сумм Б.Д., Горюнов Ю.В. Физико-химические основы смачивания и растекания. – М.: Химия, 1976. – 232 с.
- Fowkes F.M. Dispersion Force Contributions to Surface and Interfacial Tensions, Contact Angles, and Heats of Immersion. //Advances in Chemistry Series. American Chemical Society, Washington. - 1964. - № 43. - P. 99-111.
- De Gennes P.G. Wetting: Statics and Dynamics. //Rev. Mod. Phys. - 1985. - V.57. - P.827-863.
- Owens D.K., Wendt R.C. Estimation of the Surface Free Energy of Polymers. // J. Appl. Polym. Sci. - 1969. - V.13. - P. 1741-1747.
- Verkholomov V.K. Physical Features of the New Equation (Equation Jung - Verkholomov) of Contact Angle. // Materials of the XII international research and practice conference «Science, Technology and Higher Education». – December 21-22, 2016. – Westwood, Canada. – P. 97-110.
- Zisman W.A. Relation on the Equilibrium Contact Angle to Liquid and Solid Constitution. // Advances in Chemistry Series. American Chemical Society, Washington. 1964. №43. - P. 1-51.
- Жалоба
- 1 647
- syshatunov от