On adhesion work at wetting solid surface by liquid phase (EN) / О работе адгезии при смачивании твердой поверхности жидкой фазой (RU)
В. К. Верхоломов
Аннотация
Исходя из механической модели для системы твердое тело/жидкость/пар получено новое уравнение работы адгезии при смачивании твердой поверхности жидкой фазой. Показано, что известное уравнение Юнга-Дюпре по форме является частным случаем нового уравнения Юнга-Верхоломова краевого угла смачивания.
// Science and World. 2017, № 4, V. 1, p. 11-14
Введение
Известно, что смачивание жидкой фазой твердой поверхности определяется физико-химическими процессами, протекающими на границах раздела фаз, участвующих в смачивании [1,2].
В теории смачивания важной характеристикой происходящих процессов служит величина равновесного краевого угла смачивания θ0. Она позволяет судить, например, о гидрофобности/гидрофильности той или иной твердой поверхности, а также о том, как изменяются эти характеристики при воздействии различных внешних факторов (влажности, температуры и др.) [3,4]. В то же время следует отметить, что имеющиеся экспериментальные данные по краевым углам смачивания входят в противоречие с некоторыми положениями теории смачивания и, в первую очередь, с классическим уравнением Юнга. Более того, если можно так выразиться, уравнение Юнга стало определенным тормозом при разработке новых гладких покрытий, в первую очередь, с большими краевыми углами (θ0 >1300).
В теории смачивания существуют два подхода для оценки системы твердое тело/жидкость/пар и, соответственно, для определения краевого угла смачивания: механический и термодинамический.
Отметим, что у истоков первого (механического) подхода стоял Т. Юнг. В соответствии с этим подходом величина равновесного краевого угла определяется соотношением двух сил, действующих на линии смачивания (линии трехфазного контакта) капли жидкости, помещенной на твердую поверхность: сил адгезии и сил когезии [5]. Таким образом, Юнг рассматривал систему твердое тело / жидкость / пар, как разновидность изолированной механической системы, основанной на взаимодействии сил.
У истоков второго (термодинамического) подхода стоял У. Гиббс. В соответствии с этим подходом исследуемая система рассматривается, как изолированная термодинамическая система. Для таких систем справедливо одно из основных положений термодинамики: в состоянии равновесия потенциальная энергия системы минимальна.
Согласно существующей теории смачивания считаются правильными оба подхода: и механический, и термодинамический [1,2]. Тем не менее, термодинамический подход считается более полным, а потому более предпочтительным. На его основе, было получено уравнение равновесного краевого угла – уравнение Юнга.
В соответствии с новой предлагаемой концепцией такое положение, когда признаются правильными оба подхода, считается неприемлемым, ибо оба подхода являются взаимоисключающими друг друга. Одно из двух: или рассматриваемая система – термодинамическая, или она – разновидность механической системы. В работах [6,7] было показано, что систему твердое тело/жидкость/пар нельзя рассматривать в качестве термодинамической. Она является разновидностью изолированной механической системы. Поскольку классическое уравнение Юнга краевого угла получено в рамках термодинамического подхода, то оно требует пересмотра.
Целями настоящей работы было определение уравнения для работы адгезии WA. Прежнее уравнение для WA было получено Дюпре исходя из термодинамического подхода, а потому его нельзя считать правильным.
1. Особенности изолированной механической системы
Главной физической особенностью изолированной механической системы является то, что между ее телами происходит силовое взаимодействие и обмен энергией только в механической форме (потенциальной или кинетической). Закон сохранения энергии, в общем случае перемещения тел с большими скоростями, может быть сформулирован в следующем виде: сумма потенциальной и кинетической энергий тел в изолированной системе сохраняется неизменной. В частном случае перемещения тел с небольшими скоростями сохраняется неизменной сумма их потенциальных энергий.
Изолированная система твердое тело/жидкость/пар является разновидностью механической системы, в которой между телами происходит силовое взаимодействие и обмен механической потенциальной энергией. Следует отметить, что механическая потенциальная энергия тела не мыслима без присущей ей консервативной силы, стремящейся уменьшить ее до минимума. Так, например, потенциальная энергия тела, поднятого над поверхностью, связана с силой притяжения к земле. Потенциальная энергия растянутой пружины связана с силой упругости. Потенциальная энергия поверхностного натяжения жидкости (воды, мыльной пленки) связана с силой поверхностного натяжения и т.д.
Хотелось бы особо подчеркнуть, что механическая система представляет систему взаимодействующих тел, т.е. тела в системе находятся на таком расстоянии друг от друга, при котором между ними происходит силовое взаимодействие и обмен энергией. В механической системе между телами происходит постоянное взаимодействие.
В процессе взаимодействия тел в изолированной механической системе главную, основную роль играет взаимодействие их сил. Равновесие изолированной системы наступает тогда, когда равнодействующая всех сил, действующих в системе, становится равной нулю.
2. Уравнение Юнга-Верхоломова краевого угла смачивания
Пересмотр уравнения краевого угла проведен в рамках механического подхода, основываясь на представлениях Юнга о силах адгезии и когезии, действующих на линии смачивания. Новое уравнение краевого угла, названное в [7] уравнением Юнга-Верхоломова, имеет следующий вид:
Cos θ0=(σA–σLS)/σLV , (1)
где σA – сила адгезии твердой поверхности на границе с паром; σLS, σLV – силы поверхностного натяжения жидкости на границах раздела жидкость/твердое тело и жидкость/пар соответственно.
Хотелось бы еще раз особо подчеркнуть, что сила адгезии σA возникает лишь в месте контакта капли жидкости с поверхностью твердого тела, и ее область действия, в отличие от свободной поверхностной энергии σSV, имеет ограниченные размеры.
В работе [7] было показано, что величину σLS можно определить с помощью следующего выражения:
σLS= σL0 – σA0 , (2)
где σL0 – сила поверхностного натяжения жидкости в случае, когда давление насыщенного пара близко к нулю (именно этот случай реализуется на границе жидкость/твердое тело); σA0 – сила адгезии на границе твердое тело/вакуум.
Величины σL0, σA0 можно представить в следующем виде:
σA0= σA + ΔσA (3)
σL0= σLV + ΔσLV , (4)
где σA, σLV – силы адгезии и поверхностного натяжения на границах раздела твердое тело/пар и жидкость/пар соответственно: см. уравнение (1);
ΔσA – превышение силы адгезии (превышение σA0 над σA); ΔσLV – превышение силы поверхностного натяжения. Здесь мы говорим о превышениях в алгебраическом смысле, т.е. в общем случае величина соответствующего превышения может быть как положительной, так и отрицательной.
Подставляя (2), (3), (4) в уравнение (1), получим
Cos θ0 = (2σA – σLV)/σLV + (ΔσA - ΔσLV)/ σLV . (5)
В случае, когда σA>> ΔσA и σLV>> ΔσLV, вторым членом в уравнении (5) можно пренебречь и получим следующее приближенное уравнение Юнга-Верхоломова краевого угла смачивания
Cos θ0 ≈ (2σA – σLV)/σLV . (6)
Уравнения (1) и (6), в первую очередь, следует рассматривать, как уравнения баланса сил, каждая из которых отнесена к единице длины линии смачивания. Если числитель и знаменатель этих уравнений умножить на единицу площади, то получим уравнения баланса энергий. В этом случае величины σA и σLV следует рассматривать, как удельные потенциальные энергии адгезии и поверхностного натяжения. Таким образом, получается, что новые уравнения краевого угла являются и уравнениями баланса сил, и уравнениями баланса энергий. Аналогичный вывод был сделан ранее в отношении величины поверхностного натяжения [8]: энергия поверхностного натяжения жидкости эквивалентна силе поверхностного натяжения. Таким образом, если речь идет о единице длины линии смачивания, то имеет место сила поверхностного натяжения, если – о единице площади поверхности жидкости, то – энергия поверхностного натяжения. Вполне логично, что такое же эквивалентное соотношение существует между силой адгезии и поверхностной энергией адгезии.
3. Уравнение работы адгезии
На основании термодинамического подхода к системе твердое тело / жидкость / пар Дюпре получил следующее уравнение работы адгезии:
WA = σSV + σLV - σSL , (7)
где σSV, σLV, σSL – поверхностные энергии на границах раздела фаз твердое тело/пар, жидкость/пар и твердое тело/жидкость соответственно.
Как известно, термодинамический подход не предполагает никакого силового взаимодействия между телами (фазами) системы. Поэтому мы можем оторвать каплю жидкости (воды), находящуюся в состоянии равновесия на твердой поверхности, и поднять, не изменяя ее формы, над поверхностью на ничтожно малое расстояние (например, на несколько микрон). А можем поднять ее на большое расстояние (например, на несколько метров). В обоих случаях уравнение (7) сохраниться неизменным.
Иная физическая картина получается в случае механической системы твердое тело/жидкость/пар. На рис. представлены два случая взаимодействия капли жидкости с твердой поверхностью. В случае а) капля жидкости сидит на твердой гидрофильной поверхности и находится в состоянии равновесия. Начальная потенциальная поверхностная энергия на границе жидкость/твердое тело в расчете на единицу площади равна
Eн = σLS= σL0 – σA0 . (8)
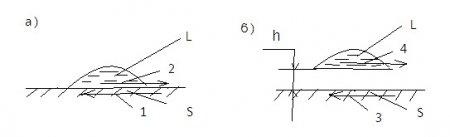
Рис. Схема взаимодействия капли жидкости с твердой поверхностью: S-твердая поверхность; L-жидкость
В случае б) каплю, не изменяя ее формы, оторвали от твердой поверхности и подняли на ничтожно малое расстояние h. На рис. стрелками также обозначены силы: 1- σA0; 2- σL0; 3- σA; 4- σLV. При отрыве капли была затрачена работа, равная работе адгезии WA. Величина образовавшегося зазора h столь мала, что осталось силовое взаимодействие между каплей жидкости и поверхностью твердого тела. (Отметим, что, если мы поднимем каплю на расстояние, значительно превышающее h, то сила адгезии исчезнет и останется лишь поверхностная энергия твердого тела σSV). Естественно, что зазор заполнился паром. Потенциальная энергия в конечном состоянии
Eк = σLV + σA . (9)
Работа адгезии получилась равной
WA = Eк – Eн = σLV + σA – (σL0 – σA0)
С учетом уравнений (3), (4) окончательно получаем
WA = 2σA + (ΔσA - ΔσLV) . (10)
В случае, когда величинами превышений можно пренебречь, имеем следующее выражение для определения приближенной величины работы адгезии:
WA ≈ 2σA . (11)
Подставляя (11) в уравнение (6), получим уравнение краевого угла
Cos θ0 ≈ (WA – σLV)/σLV . (12)
Это уравнение по форме напоминает известное уравнение Юнга-Дюпре. Таким образом, получается, что уравнение Юнга-Дюпре по форме является частным случаем уравнения Юнга-Верхоломова. Фактически получено новое уравнение Юнга-Дюпре. Принципиальным отличием нового уравнения является новое выражение для работы адгезии, полученное исходя из механической модели для системы твердое тело / жидкость / пар.
Выводы
1. Получено новое уравнение работы адгезии при отрыве капли жидкости от твердой поверхности. Оно основано на механической модели для системы твердое тело/жидкость/пар.
2. Показано, что известное уравнение Юнга-Дюпре по форме является частным случаем нового уравнения Юнга-Верхоломова. Фактически получено новое уравнение Юнга-Дюпре с новым выражением для определения величины работы адгезии.
Литература
- Сумм Б.Д., Горюнов Ю.В. Физико-химические основы смачивания и растекания. М.: Химия, 1976. 232 с.
- Григорьев Г.А. Термодинамика и кинетика смачивания и растекания. М.: МИТXТ им. М.В. Ломоносова, 2008. 76 с.
- Пашинин А.С., Емельяненко А.М., Бойнович Л.Б. Взаимодействие гидрофобных и супергидрофобных материалов с водными средами. // Физикохимия поверхности и защита материалов. 2010. Т.46. №6. С. 664-670.
- Верхоломов В.К. Экспериментальная оценка гидрофобных свойств различных покрытий. //Физика и химия обработки материалов. 2014. №3. С. 33-37.
- Сумм Б.Д. Гистерезис смачивания. // Соровский образовательный журнал. 1999. №7. С. 98-104.
- Verkholomov V.K. About the New Equation of Contact Angle. // Materials of the XI international research and practice conference "Science, Technology and Higher Education". October 19-20, 2016. Westwood, Canada. P. 138-143.
- Verkholomov V.K. Physical Features of the New Equation (Equation Jung - Verkholomov) of Contact Angle. // Materials of the XII international research and practice conference "Science, Technology and Higher Education". December 21-22, 2016. Westwood, Canada. P. 97-110.
- Адамсон А. Физическая химия поверхностей. М.: Мир, 1979. 568 с.
- Жалоба
- 1 379
- syshatunov от